本科生数学建模课程设计
学院(部)文理学院
专 业:
班 级:
姓 名:
指导教师:
完成日期:
摘要
实验设计和统计建模在现实生产中有着广泛的应用,随着计算机技术的飞速发展,其方法和理论在实践中又得到不断的完善和发展。统计建模分析法是指首先取历史实验或生产数据记录,用统计建模的方法求取输入输出变量间的数学模型,再根据数学模型及约束条件进行最优化计算,取得最优操作参数。此法所用的方程,可以是现行方程,多项式非线性方程或者其他任何形式的方程。这些形式的方程,可以根据专业人员的经验选定,业可以根据实际数据由算法具体确定。他们的选用,系根据经验判断或统计分析的结果,可以完全没有理论依据。
案例背景:
钢铁制造业有两种类型的钢铁需要制造(钢铁1和钢铁2)并且有两种生产方案(方案1和方案2)。在生产钢铁的时候共用到三种类型的资源:铁矿石,煤炭,高炉时间。两种加工方案用到不同类型的高炉,所以方案的不同使用到的加工资源的量也会不同。
|
生产一吨的产品 |
铁矿石的需求量(吨) |
煤炭的需求量(吨) |
需要高炉时间(小时) |
|
钢铁1用方案1生产 |
8 |
3 |
2 |
|
钢铁2用方案1生产 |
6 |
1 |
1 |
|
钢铁1用方案2生产 |
7 |
3 |
1 |
|
钢铁2用方案2生产 |
5 |
2 |
1 |
每天,有12吨的煤炭供给方案1,15吨的煤炭供给方案2,煤炭不可以在方案之间转移。每天方案1有10个小时的高炉加工时间,方案2有有4个小时的高炉加工时间。每天总共有80吨的铁矿石供给方案1和方案2。钢铁1每吨的出售价格是170元,钢铁2每吨的出售价格是160元。所有的钢铁都销售给同一个顾客。方案1的运输费用是每吨80元,方案2的运输费用是每吨100元。
X1=钢铁1使用方案1的生产量
X2=钢铁2使用方案1的生产量
X3=钢铁1使用方案2的生产量
X4=钢铁2使用方案2的生产量
利润表达式为170(x1 +x3)+160(x2+x4);成本表达式为80(x1+x2)+100(x3+x4)
目标函数z=90×1 + 80×2 + 70×3 + 60×4
约束:
3×1 + x2 <=12 (方案1每天最多得到12吨的煤炭)
2×1 + x2 <=10 (方案1每天最多用10个小时的高炉时间)
3×3 + 2×4 <=15 (方案2每天最多得到15吨煤炭)
X3 + x4 <=4 (方案2每天对多用4个小时的高炉时间)
8×1 + 6×2 + 7×3 + 5×4 <=80 (两种方案每天最多得到80吨的铁矿石)
用LINGO求解上述问题
LINGO的源代码如下:
model:
sets:
ii/1..4/:x,c;
jj/1..5/:b;
link(jj,ii):a;
endsets
data:
c=-90,80,70,60;
b=12 10 15 4 80;
a=3 1 0 0
2 1 0 0
0 0 3 2
0 0 1 1
8 6 7 5;
enddata
max=@sum(ii(i):x(i)*c(i));
@for(jj(j):@sum(ii(i):a(j,i)*x(i))<=b(j));
求解结果为:
Objective value: 1040.000
Variable Value Reduced Cost
X( 1) 0.000000 202.0000
X( 2) 10.00000 0.000000
X( 3) 0.000000 14.00000
X( 4) 4.000000 0.000000
进行灵敏度分析,其结果为:
Ranges in which the basis is unchanged:
Objective Coefficient Ranges:
Current Allowable Allowable
Variable Coefficient Increase Decrease
X( 1) -90.00000 202.0000 INFINITY
X( 2) 80.00000 INFINITY 8.000000
X( 3) 70.00000 14.00000 INFINITY
X( 4) 60.00000 6.666667 10.00000
Righthand Side Ranges:
Current Allowable Allowable
Row RHS Increase Decrease
2 12.00000 INFINITY 2.000000
3 10.00000 2.000000 0.000000
4 15.00000 INFINITY 7.000000
5 4.000000 INFINITY 0.000000
6 80.00000 0.000000 20.00000
目标函数值为1040,决策变量的取值为:
X1=0; x2=10; x3=0; x4=4.
结论:在给出案例背景之后,通过建立线性约束方程来进行求解,通过所学lingo软件来对原问题进行求解。可以很快地得出目标函数值。这使我进一步的对此软件的了解和使用。
Spss分析
摘要
单现象描述分析(简单描述分析),是对客观事物单方面特征进行描述的分析。对客观事物的描述方法(分析方法),以其手段的不同归纳起来可以有指标描述法、表格描述法、图形描述法、推断描述法等。指标描述法,是以统计指标方式来认识事物,认识的具体内容包括集中趋势、离中趋势、分布特征等。相关的SPSS方法主要是描述统计中的描述,除此之外还有描述统计中的频率、探索两方法。这些分析的特点是输出统计指标。表格描述法,是以分组表的方式来描述事物的特征,其内容仅包括简单分布表(交互分布表属多现象描述分析)。相关SPSS方法是描述统计中的频率,其特点是输出频率表。图形描述法,是以统计图方式来认识事物的特征,其内容包括箱索图、茎叶图、饼图、条形图、直方图、散点图等。相关的SPSS方法是描述统计中的探索、频率方法和图形菜单中的各种图形功能。探索功能可输出箱索图和茎叶图。频率功能可输出饼图、条形图和直方图。图形功能则可输出除茎叶图外的各种图。推断描述法,是以数据库中的样本数据为依据,推断总体特征。尽管此处的总体事物超出SPSS中的样本范围,但人们也只不过将其看作是更大的样本罢了。从认识目的来看,推断描述中对总体均值、比率或方差的认识仍属表面认识。统计抽样推断的具体内容包括统计估计和假设检验两种。统计估计的主要内容就是完成总体均值、成数的区间估计,相关的SPSS分析方法是描述统计中的探索功能。假设检验的主要内容是均值、成数假设检验,相关的SPSS分析方法是均值比较中的单样本T检验
下面给出了某地区1971-2000年的人口变化情况:
|
年份 |
时间变量 |
人口 |
|
1971 |
1 |
33815 |
|
1972 |
2 |
33918 |
|
1973 |
3 |
34004 |
|
1974 |
4 |
34165 |
|
1975 |
5 |
34212 |
|
1976 |
6 |
34327 |
|
1977 |
7 |
34344 |
|
1978 |
8 |
34458 |
|
1979 |
9 |
34498 |
|
1980 |
10 |
34476 |
|
1981 |
11 |
34483 |
|
1982 |
12 |
34488 |
|
1983 |
13 |
34513 |
|
1984 |
14 |
34497 |
|
1985 |
15 |
34511 |
|
1986 |
16 |
34520 |
|
1987 |
17 |
34507 |
|
1988 |
18 |
34509 |
|
1989 |
19 |
34521 |
|
1990 |
20 |
34513 |
|
1991 |
21 |
34515 |
|
1992 |
22 |
34517 |
|
1993 |
23 |
34519 |
|
1994 |
24 |
34519 |
|
1995 |
25 |
34521 |
|
1996 |
26 |
34521 |
|
1997 |
27 |
34523 |
|
1998 |
28 |
34525 |
|
1999 |
29 |
34525 |
|
2000 |
30 |
34527 |
上表中的数据,我们可以做出时间变量与人口的关系;利用spss对上述数据进行非线性回归分析。具体操作步骤如下图所示:
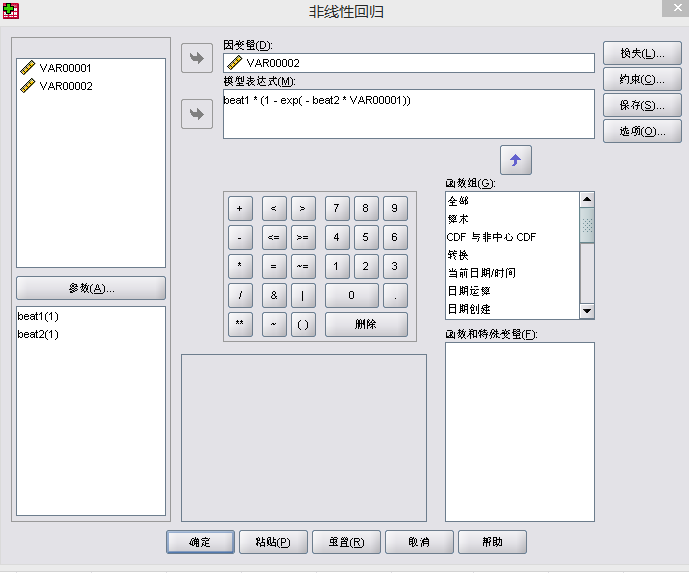
上图是操作的步骤,下面是输出的结果:
所以函数表达式为:
Y=34416.367(1-exp(-358.000x))
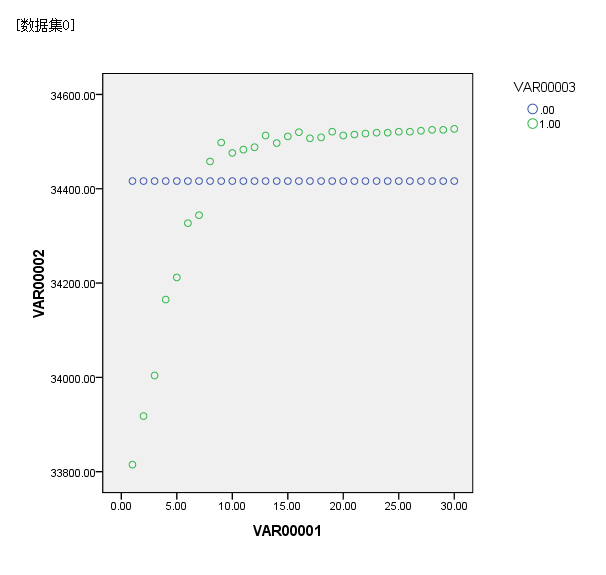
再做出散点图如下图所示:
结论:根据上表提供的数据,我们对城市的人口随着时间的增长做出了非线性回归预测,得到函数表达式,并且做出了散点图和预测的数据进行对比。
