2018春季统计分析研究课题
注:如果响应变量的个数比较少,可以逐个拟合模型。如果响应变量的个数较多,可以:
1. 重新整合数据集:将全部响应变量拉直到一个变量Y中,在数据集中加入一个名义变量用于指示响应变量。如加入名义变量index, index="1"时,对应的Y是第一个响应变量的值; index="2"时,对应的Y是第二个响应变量的值,等等。这样只需要考虑Y和原先所有自变量以及index的建模就可以了。
2. 将响应变量进行压缩:利用主成分或其他方法将响应变量压缩成少数几个综合响应变量,然后用这些综合响应变量对所有自变量建模。
背景及统计的作用:
一个洗衣粉产品的清洁能力好坏受很多因素的影响,例如:
1. 配方中的每一成分的多少
2. 洗衣的方法及环境条件(洗衣时间的长短,洗衣用水的情况等)
如果能通过统计建模的方法建立一个用配方及洗衣条件来预测产品功效的模型,就可以
1. 了解产品中每一成分,及洗衣的方法、条件等因素对产品清洁能力的影响;
2. 在给出产品的配方时对产品在一定条件下的清洁能力做出比较可靠的预测;
3. 在一定的条件下,优化产品的配方。
试验:
根据目标,我们设计了一个250个不同处理组合(Treatment)的试验:
1. 设计时考虑的因素有产品的配方中每一成分的量及洗衣条件,每一因素有三个水平;
2. 用设计所得的每一个配方的产品去洗涤一些衣物,根据洗涤后衣物的清洁程度计算出每一配方的清洁能力(试验中衣物的初始脏度可能会有一些波动,所以拟合模型时需要考虑到它的影响);
3. 每四个配方作为一组来进行试验(这样就产生了一个区组的效应需要在建模时考虑);
已有的数据:
250个不同处理组合(Treatment)的试验数据
输入变量包括:
1. 配方中的20种成分 (C1—C20)
2. 洗衣方法及洗衣环境参数 4 个 (P1—P4)
3. 区组 (block)
4. 衣物初始的脏度 (Baseline1—Baseline5,分别对应5种污渍)
输出变量为:产品在5种不同种类污渍上的清洁功效(Cleaning1—Cleaning5)
要求:
1. 对此数据选用不同的统计方法进行分析,建立一个用产品配方来预测产品清洁能力模型;
2. 需要考虑的效应为所有变量的线性项,C1—C20、P1—P4的平方项及交互作用项;
3. 将对应每一污渍初始的脏度(Baseline1—Baseline5)作为协变量放入模型,例如对Cleaning1建模时,需将Baseline1作为协变量加入模型,依此类推;
4. 试用多种不同的模型选择方法对数据进行分析;
5. 选择合适的能够反映模型预测能力的评价准则(可以根据需要提出新的准则),并根据所选准则找出最优模型;
6. 再利用前10组数据说明拟合出的模型的预测能力。
注意:
如果同时考虑所有的线性项、平方项和交互作用项的话,所有要估计的参数的个数远大于处理组合的个数(250)。
1、数据整理
因为污渍初始脏度(Baseline1-Baseline5)要作为协变量,于是重新整合数据集,将全面相应变量(Cleaning1-Cleaning5)拉到一个变量cleaning中,并对应在解释变量数据集中加入一个名义变量index。当index=1,对应Baseline1, Cleaning1;当index=2,对应Baseline2, Cleaning2;依此类推。另外将block, C1-C20, P1-P4复制4次,将250个样本数据拉到了1250个。
同时注意到,当固定block值,P2值为常值,故在接下来的建模过程中剔除这一变量。
这里有一篇关于数据导入的文章,如果你不懂数据导入的话!——–传送门
R语言教程之如何导入数据
2、统计建模
2.1 只考虑线性项
lm(formula = cleaning ~ factor(block) + C1 + C2 + C3 + C4 + C5 + C6 + C7 + C8 + C9 + C10 + C11 + C12 + C13 + C14 + C15 + C16 + C17 + C18 + C19 + C20 + P1 + P3 + P4 + factor(index) + baseline, data = laundry) Residual standard error: 9.303 on 1159 degrees of freedom Multiple R-squared: 0.8202, Adjusted R-squared: 0.8062 F-statistic: 58.74 on 90 and 1159 DF, p-value: < 2.2e-16
R-squared为0.8202,表示解释变量可以解释相应变量82.02%的信息。P-value小于0.05,因此回归方程的检验是显著的。
2.2 考虑二次项和交叉项
lm(formula = cleaning ~ factor(block) + C1 + C2 + C3 + C4 + C5 + C6 + C7 + C8 + C9 + C10 + C11 + C12 + C13 + C14 + C15 + C16 + C17 + C18 + C19 + C20 + P1 + P3 + P4 + factor(index) + baseline +C1^2 + C2^2 + C3^2 + C4^2 + C5^2 + C6^2 + C7^2 + C8^2 + C9^2 + C10^2 + C11^2 + C12^2 + C13^2 + C14^2 + C15^2 + C16^2 + C17^2 + C18^2 + C19^2 + C20^2 + P1^2 + P3^2 + P4^2 + C1 * P1 + C1 * P3 + C1 * P4 + C2 * P1 + C2 * P3 + C2 * P4 + C3 * P1 + C3 * P3 + C3 * P4 + C4 * P1 + C4 * P3 + C4 * P4 + C5 * P1 + C5 * P3 + C5 * P4 + C6 * P1 + C6 * P3 + C6 * P4 + C7 * P1 + C7 * P3 + C7 * P4 + C8 * P1 + C8 * P3 + C8 * P4 + C9 * P1 + C9 * P3 + C9 * P4 + C10 * P1 + C10 * P3 + C10 * P4 + C11 * P1 + C11 * P3 + C11 * P4 + C12 * P1 + C12 * P3 + C12 * P4 + C13 * P1 + C13 * P3 + C13 * P4 + C14 * P1 + C14 * P3 + C14 * P4 + C15 * P1 + C15 * P3 + C15 * P4 + C16 * P1 + C16 * P3 + C16 * P4 + C17 * P1 + C17 * P3 + C17 * P4 + C18 * P1 + C18 * P3 + C18 * P4 + C19 * P1 + C19 * P3 + C19 * P4 + C20 * P1 + C20 * P3 + C20 * P4, data = laundry)
Multiple R-squared: 0.8239, Adjusted R-squared: 0.7999
在加入C1-C20, P1-P4的二次项及这两个类的交叉项后,发现Adjusted R-squared反而下降了,说明加了更多解释变量,对清洁能力的解释程度并没出现较大幅度上升。据此,最后我们不会考虑二次项和交叉项。
2.3 逐步回归
考虑到(1)中有些回归系数不显著,因此我们通过逐步回归,以AIC信息统计量为准则,选择最小的AIC信息统计量来达到删除变量的目的。Step回归后的解释变量为:
cleaning ~ factor(block) + C1 + C6 + C13 + C14 + P1 + P4 + factor(index) C1 7.0379 0.7362 9.560 < 2e-16 *** C6 3.6791 0.8000 4.599 4.71e-06 *** C13 1.3765 0.7748 1.777 0.07589 . C14 1.1788 0.7462 1.580 0.11441 P1 -4.0575 0.7812 -5.194 2.43e-07 *** P4 6.1982 0.7479 8.288 3.12e-16 *** factor(index)2 -37.0104 0.8291 -44.640 < 2e-16 *** factor(index)3 9.6095 0.8291 11.590 < 2e-16 *** factor(index)4 3.8324 0.8291 4.622 4.21e-06 *** factor(index)5 -26.9762 0.8291 -32.537 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 9.269 on 1177 degrees of freedom Multiple R-squared: 0.8187, Adjusted R-squared: 0.8076 F-statistic: 73.83 on 72 and 1177 DF, p-value: < 2.2e-16
回归系数检验的显著水平得到了很大的提高,但是C14的显著性检验仍没有通过,因此我们直接删除C14,并确定最后的预测模型。
2.4 最终模型
Final model: cleaning ~ factor(block) + C1 + C6 + C13 + P1 + P4 + factor(index)
方差膨胀因子检验:
> vif(lm.final) GVIF Df GVIF^(1/(2*Df)) factor(block) 5.030919 62 1.013114 C1 1.357311 1 1.165037 C6 1.493310 1 1.222011 C13 1.340551 1 1.157822 P1 1.326220 1 1.151616 P4 1.430880 1 1.196194 factor(index) 1.000000 4 1.000000
因为每个GVIF^(1/(2*Df))均小于10,所以可以判定不存在多重共线性。下图左上角为残差散点图,右上角为Q-Q Plot,左下角为标准化残差绝对值的开方的残差图,右下角为Cook距离图。
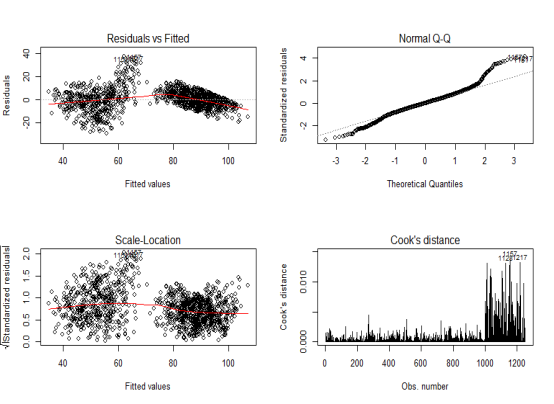
最终我们以现有数据作为测试集,计算MSE,最后结果为86.03.
版权所有,转载请注明出处!

