F79MA 2018-19: Assessed Project 1 Report
Introduction and Summary
This project is aim to look at parameter estimation for an inverse gamma model, which can be considered as a survival distribution. Also, we will show that computer simulation can be a very useful tool to characterize the performance of statistical estimators.
Analysis
The probability density function of inverse distribution is
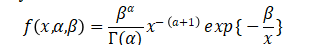
where 
is a shape parameter, is a scale parameter, and is the gamma function.
Let be a random sample from an inverse gamma distribution with shape parameter and unknown scale parameter .
Task 1
As is i.i.d, the joint density function is
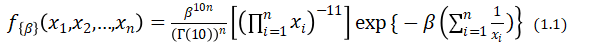
Then
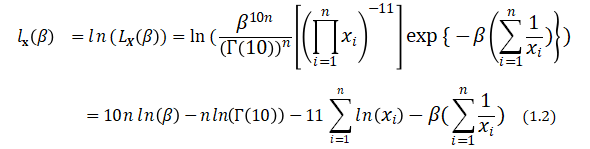
Differentiating with respect to , we get the likelihood equation
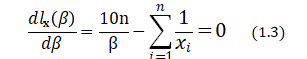
Differentiating again, we get
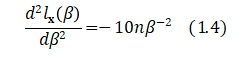
Which is negative for all , and any n.
Solving equation (1.3) for , we get
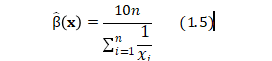
因部分公式不兼容请查看doc文档
r code：
rm(list=ls(all=TRUE))
library('invgamma')
# task 3
alpha<-10 beta<-1 #true value ntime<-1000 nmax<-50 betahat<-rep(0,ntime) vac<-rep(0,nmax) MSE<-rep(0,nmax) for (n in 1:nmax){ # repeat times for (t in 1:ntime){ Y<-rinvgamma(n,alpha,rate=1) betahat[t]<-alpha/mean(1/Y) } vac[n]<-var(betahat) MSE[n]<-1/ntime*sum(betahat-beta)^2 } n<-c(1:50) plot(n,MSE,main='MSE vs n') # task 5 crbound<-beta^2/alpha/n^2 plot(MSE-crbound) abline(h=0,col='red') # task 6 betas<-c(0.3,0.5,0.8,1,1.2) MSEMME<-matrix(0,nrow=5,ncol=3) MSEMLE<-matrix(0,nrow=5,ncol=3) ns<-c(20,40,60) for (i in 1:5){ beta<-betas[i] for (j in 1:3){ n<-ns[j] mme<-rep(0,100) mle<-rep(0,100) for (t in 1:100){ sp<- rinvgamma(n,alpha,beta) mme[t]<-mean(sp)*((mean(sp))^2/var(sp)+1) mle[t]<-alpha/mean(1/sp) } MSEMME[i,j]<-1/100*sum((mme-beta)^2) MSEMLE[i,j]<-1/100*sum((mle-beta)^2) } } round(MSEMME,4) round(MSEMLE,4) # task 7 betas<-c(0.3,0.5,0.8,1,1.2) AVsMLE<-matrix(0,nrow=5,ncol=3) ns<-c(20,40,60) for (i in 1:5){ beta<-betas[i] for (j in 1:3){ n<-ns[j] mle<-rep(0,100) for (t in 1:100){ sp<- rinvgamma(n,alpha,beta) mle[t]<-alpha/mean(1/sp) } AVsMLE[i,j]<-sd(mle) } } round(AVsMLE,4)