数据预处理惩罚中的缺失值问题

1. 简介1.1 缺失值的分类缺失值从数据漫衍上可被分为三类 (Gelman and Hill 2006, Little and Rubin (2002)) ：missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR)。完全随机缺失（MCAR）：某一变量缺失值不依赖于其他任何原因的完全随机缺失随机缺失（MAR）：某一变量的缺失与其他变量相关但与该变量自己的数值不相关非随机缺失（NMAR）：某一变量的缺失和该变量自己的数值相关， e.g., 仪器的较低检测线：某被检测物质的含量低于该检测线则会发生非随机缺失(left-censored missing)
今朝大部门填补缺失值的要领都是基于MCAR和MAR，这两种环境也相比拟力难区别，因此本文会将这两种环境归并起来接头。
1.2 缺失值的可视化我一般拿到数据的第一件事就是用Amelia package (Honaker, King, and Blackwell 2011) 内里的missmap function看一下缺失值的漫衍环境。require(magrittr)require(Amelia)load(file=”MVI.RData”)missmap(test_na, col=c(“black”, “grey”), legend=FALSE, main = ‘Missing Map’)

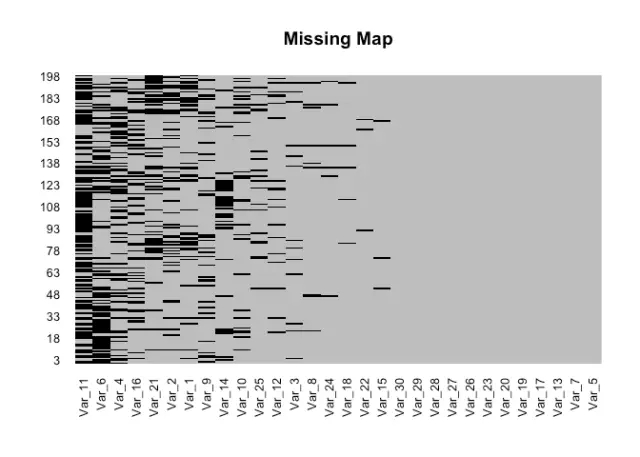
# 对付某一变量的缺失值识别可用is.na()sum(is.na(test_na$Var_1))## [1] 43
1.3 为什么要对缺失值举办处理惩罚对付MCAR，直接删除缺失的样本一般不会对功效发生毛病，但会淘汰样本数量；对付非完全随机确实出格是MNAR，假如缺失值较多则会对功效发生很大的偏移。另一方面，许多后续的统计检讨要求完整的没有缺失值的数据集, e.g., principal components analysis (PCA).
2. 今朝常用的缺失值处理惩罚要领2.1 行删除2.1.1 直接删除有缺失值的样本最简朴粗暴的要领就是直接na.omit()，可是我们可以看到本来198个样本被删到了只剩4个。
test_na_rm <- na.omit(test_na)dim(test_na)## [1] 198  30dim(test_na_rm)## [1]  4 30
2.1.2 80%法例80%法例 (Bijlsma et al. 2006)认为，当某一物质的非缺失部门低于总样本量的80%时，发起删除该物质。Modified 80%法例认为， 当某一物质的非缺失部门低于所有生物学亚组的80%时，发起删除该物质。# remove variables with missing > 20% mis_prop <- sapply(test_na, function(x) sum(is.na(x))/length(x))var_rm <- names(mis_prop)[mis_prop > 1 – 0.8]var_rm # remove 7 variables## [1] “Var_1”  “Var_2”  “Var_4”  “Var_6”  “Var_11” “Var_16” “Var_21″test_na_rm <- test_na[, !colnames(test_na) %in% var_rm]test_na_rm <- na.omit(test_na_rm)dim(test_na)## [1] 198  30dim(test_na_rm)## [1] 83 23去掉7个不切合80%法例的物质今后再用na.omit()删除有缺失的样本，最终的样本数量维持在了83个。
2.2 单变量填补用单一变量的均值/中位数/二分之一最小值/零值举办补值，这种要了解导致数据漫衍的偏移，方差偏小，PCA上会看到一条补值导致的直线等问题。
2.2.1 MCAR/MAR对付MCAR/MAR，可以用均值/中位数补值。# meantest_na_mean_imp <- lapply(test_na, function(x) {    x[is.na(x)] <- mean(x, na.rm = T)    x  })test_na_mean_imp_df <- do.call(cbind.data.frame, test_na_mean_imp)# mediantest_na_median_imp <- lapply(test_na, function(x) {    x[is.na(x)] <- median(x, na.rm = T)    x  })test_na_median_imp_df <- do.call(cbind.data.frame, test_na_median_imp)
2.2.2 MNAR对付left-censored MNAR可以用二分之一最小值/零值举办补值。# half of minimumtest_na_hm_imp <- lapply(test_na, function(x) {    x[is.na(x)] <- min(x, na.rm = T)/2    x  })test_na_hm_imp_df <- do.call(cbind.data.frame, test_na_hm_imp)# zerotest_na_zero_imp_df <- test_natest_na_zero_imp_df[is.na(test_na_zero_imp_df)] <- 0
2.3 多变量填补多变量填补的前提是其他变量对付该变量的可预测性，用其他变量作为independent variable，含有缺失值的该变量作为dependent variable，成立模子，用模子来预测该变量中的缺失值。
2.3.1 MCAR/MAR今朝常用的补值要领大部门都是针对MCAR/MAR的环境：missForest (Stekhoven and Bühlmann 2012), k-nearest neighbors (kNN) (Troyanskaya et al. 2001), singular value decomposition (SVD) (T. Hastie, Tibshirani, and Sherlock 1999, Stacklies et al. (2007)), 等等。# 请先安装missForest packagerequire(missForest)# missForesttest_na_missForest_imp_df <- missForest(test_na)[[1]]##   missForest iteration 1 in progress…done!##   missForest iteration 2 in progress…done!##   missForest iteration 3 in progress…done!##   missForest iteration 4 in progress…done!##   missForest iteration 5 in progress…done!# 请先安装impute packagerequire(impute)# kNNtest_na_kNN_imp_df <-  test_na %>% data.matrix() %>% impute.knn() %>% extract2(1) %>% data.frame()# 请先安装imputeLCMD packagerequire(imputeLCMD)# SVDSVD_wrapper <- function(data, K = 5) {  data_sc_res <- scale_recover(data, method = ‘scale’)  data_sc <- data_sc_res[[1]]  data_sc_param <- data_sc_res[[2]]  result <- data_sc %>% impute.wrapper.SVD(., K = K) %>%     scale_recover(., method = ‘recover’, param_df = data_sc_param) %>% extract2(1)  return(result)}test_na_SVD_imp_df <- SVD_wrapper(test_na) %>% data.frame()
2.3.2 MNAR今朝对付MNAR的算法开拓很是有限，如quantile regression imputation of left-censored data (QRILC) (Lazar et al. 2016), gibbs sampler based left-censored missing value imputation approach (GSimp) (Wei et al. 2017).# 请先安装imputeLCMD packagerequire(imputeLCMD)# QRILCQRILC_wrapper <- function(data, …) {  zero_idx <- which(data == 0, arr.ind = T)  data_temp <- data  data_temp[zero_idx] <- NA  result <- data_temp %>% log() %>% impute.QRILC(., …) %>% extract2(1) %>% exp()  result[zero_idx] <- 0  return(result)}test_na_QRILC_imp_df <- QRILC_wrapper(test_na)# GSimpsource(‘GSimp.R’)sim_GS_wrapper <- function(data) {  result <- data %>% multi_impute(., iters_each=50, iters_all=10, initial=’qrilc’,                                   lo=-Inf, hi=’min’, n_cores=1, imp_model=’glmnet_pred’)  return(result$data_imp)}test_na_GSimp_imp_df <- sim_GS_wrapper(test_na)## Iteration 1 start…end!## Iteration 2 start…end!## Iteration 3 start…end!## Iteration 4 start…end!## Iteration 5 start…end!## Iteration 6 start…end!## Iteration 7 start…end!## Iteration 8 start…end!## Iteration 9 start…end!## Iteration 10 start…end!Core functions for GSimp are available at: GitHub（地点：https://github.com/WandeRum/GSimp）
3. 差异补值要领的功效较量请参考以下两篇文章： Missing Value Imputation Approach for Mass Spectrometry-based Metabolomics Data (Wei et al. 2017)， GSimp: A Gibbs sampler based left-censored missing value imputation approach for metabolomics studies (Wei et al. 2017)。功效显示：在代谢组学的数据中，对付MCAR/MAR的缺失，推荐利用missForest举办补值； 对付left-censored MNAR的缺失，推荐利用GSimp举办补值。 注：以上要领还需在其他范例的数据中举办系统性的较量。
4. 缺失值补值可视化软件 – MetImp我们将以上各类补值要领 (GSimp很快也会添加进去) 做成了一个免费的web-tool: MetImp（地点：https://metabolomics.cc.hawaii.edu/software/MetImp/）Step 1: 上传数据，数据名目请保持和我们网站上example data一致； 即横行为样本，纵列为物质，第一行为物质名称，第一列为样本名称，第二列为组别信息；Step 2: 选择缺失值是属于MCAR/MAR， 照旧MNAR；Step 3: 选择物质删除尺度，非缺失部门低于总样本量的百分之几多时删除该物质；Step 4: Run；Step 5: 下载补值后的完整数据。请cite我们的文章：Runmin Wei, Jingye Wang, Mingming Su, Erik Jia, Tianlu Chen, and Yan Ni.”Missing Value Imputation Approach for Mass Spectrometry-based Metabolomics Data.” Scientific Reports (under revision).Runmin Wei, Jingye Wang, Erik Jia, Tianlu Chen, Yan Ni, and Wei Jia.“GSimp: A Gibbs sampler based left-censored missing value imputation approach for metabolomics studies.” PLOS Computational Biology (under revision).
5. 参考文献Bijlsma, Sabina, Ivana Bobeldijk, Elwin R. Verheij, Raymond Ramaker, Sunil Kochhar, Ian A. Macdonald, Ben Van Ommen, and Age K. Smilde. 2006. “Large-scale human metabolomics studies: A strategy for data (pre-) processing and validation.” Analytical Chemistry 78 (2):567–74. https://doi.org/10.1021/ac051495j.Gelman, Andrew, and Jennifer Hill. 2006. Data analysis using regression and multilevel/hierarchical models.https://doi.org/10.2277/0521867061.Hastie, Trevor, Robert Tibshirani, and Gavin Sherlock. 1999. “Imputing missing data for gene expression arrays.” Technical Report, Division of Biostatistics, Stanford University, 1–9.Honaker, James, Gary King, and Matthew Blackwell. 2011. “AMELIA II : A Program for Missing Data.” Journal of Statistical Software 45 (7):1–54. https://doi.org/10.1.1.149.9611.Lazar, Cosmin, Laurent Gatto, Myriam Ferro, Christophe Bruley, and Thomas Burger. 2016. “Accounting for the Multiple Natures of Missing Values in Label-Free Quantitative Proteomics Data Sets to Compare Imputation Strategies.” Journal of Proteome Research 15 (4):1116–25. https://doi.org/10.1021/acs.jproteome.5b00981.Little, Roderick J a, and Donald B Rubin. 2002. Statistical Analysis with Missing Data. https://doi.org/10.2307/1533221.Stacklies, Wolfram, Henning Redestig, Matthias Scholz, Dirk Walther, and Joachim Selbig. 2007. “pcaMethods – A bioconductor package providing PCA methods for incomplete data.” Bioinformatics 23 (9):1164–7.https://doi.org/10.1093/bioinformatics/btm069.Stekhoven, Daniel J., and Peter Bühlmann. 2012. “Missforest-Non-parametric missing value imputation for mixed-type data.” Bioinformatics 28 (1):112–18. https://doi.org/10.1093/bioinformatics/btr597.Troyanskaya, O, M Cantor, G Sherlock, P Brown, T Hastie, R Tibshirani, D Botstein, and R B Altman. 2001. “Missing value estimation methods for DNA microarrays.” Bioinformatics (Oxford, England) 17 (6):520–25.https://doi.org/10.1093/bioinformatics/17.6.520.Runmin Wei, Jingye Wang, Erik Jia, Tianlu Chen, Yan Ni, and Wei Jia. 2017. “GSimp: A Gibbs sampler based left-censored missing value imputation approach for metabolomics studies.” bioRxiv. https://doi.org/10.1101/177410.Runmin Wei, Jingye Wang, Mingming Su, Erik Jia, Tianlu Chen, and Yan Ni. 2017. “Missing Value Imputation Approach for Mass Spectrometry-based Metabolomics Data.” bioRxiv. https://doi.org/10.1101/171967.
接待插手本站果真乐趣群贸易智能与数据阐明群乐趣范畴包罗各类让数据发生代价的步伐，实际应用案例分享与接头，阐明东西，ETL东西，数据客栈，数据挖掘东西，报表系统等全方位常识QQ群：81035754