第三节 用R语言举办分位数回归
（六）非线性分位数回归 这里的非线性函数为Frank copula函数。
| ## Demo of nonlinear quantile regression model based on Frank copulavFrank <- function(x, df, delta, u) # 某个非线性进程，获得的是[0,1]的值-log(1-(1-exp(-delta))/(1+exp(-delta*pt(x,df))*((1/u)-1)))/delta# 非线性模子FrankModel <- function(x, delta, mu,sigma, df, tau) { z <- qt(vFrank(x, df, delta, u = tau), df) mu + sigma*z} n <- 200 # 样本量df <- 8 # 自由度delta <- 8 # 初始参数set.seed(1989)x <- sort(rt(n,df)) # 生成基于T漫衍的随机数v <- vFrank(x, df, delta, u = runif(n)) # 基于x生成理论上的非参数对应值y <- qt(v, df) # v 对应的T漫衍统计量windows(5,5)plot(x, y, pch=”o”, col=”blue”, cex = .25) # 散点图Dat <- data.frame(x = x, y = y) # 根基数据集 us <- c(.25,.5,.75)for(i in 1:length(us)){ v <- vFrank(x, df, delta, u = us[i]) lines(x, qt(v,df)) # v为概率，计较每个概率对应的T漫衍统计量} cfMat <- matrix(0, 3, length(us)+1) # 初始矩阵，用于生存功效的系数for(i in 1:length(us)) { tau <- us[i] cat(“tau = “, format(tau), “.. “) fit <- nlrq(y ~ FrankModel(x, delta,mu,sigma, df = 8, tau = tau), # 非参数模子 data = Dat, tau = tau, # data表白数据集,tau分位数回归的分位点 start= list(delta=5, mu = 0, sigma = 1), # 初始值 trace = T) # 每次运行后是否把功效显示出来 lines(x, predict(fit, newdata=x), lty=2, col=”red”) # 绘制预测曲线 cfMat[i,1] <- tau # 生存分位点的值 cfMat[i,2:4] <- coef(fit) # 生存系数到cfMat矩阵的第i行 cat(“\n”) # 假如前面把每步的功效显示出来，则每次的功效之间添加换行符}colnames(cfMat) <- c(“分位点”,names(coef(fit))) # 给生存系数的矩阵添加列名cfMat |
功效：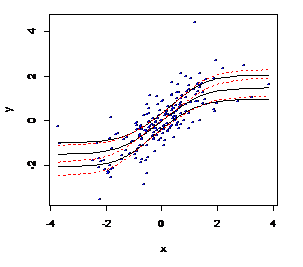
图2.5 非参数散点图、真实T漫衍和拟合功效的较量
图2.5 非参数散点图、真实T漫衍和拟合功效的较量
拟合功效：（进程略）
> cfMat
分位点 delta mu sigma
[1,] 0.25 14.87165 -0.20530041 0.9134657
[2,] 0.50 16.25362 0.03232525 0.9638209
[3,] 0.75 12.09836 0.11998614 0.9423476
（七）半参数和非参数分位数回归非参数分位数回归在局部多项式的框架下操纵起来越发利便。可以基于以下函数。
| # 2-7-1 半参数模子—-fit<-rq(y~bs(x,df=5)+z,tau=.33)# 个中bs()暗示按b-spline的非参数拟合 # 2-7-2 非参数要领lprq <-function(x,y,h,m=50,tau=0.5){ # 这是自界说的一个非参数计较函数，在其他数据下同样可以利用 xx<-seq(min(x),max(x),length=m) # m个监测点 fv<-xx dv<-xx for(i in 1:length(xx)){ z<-x-xx[i] wx<-dnorm(z/h) # 核函数为正态漫衍,dnorm计较尺度正态漫衍的密度值 r<-rq(y~z,weights=wx,tau=tau, # 上面计较获得的密度值为权重 ci=FALSE) fv[i]<-r$coef[1] dv[i]<-r$coef[2] } list(xx=xx,fv=fv,dv=dv) # 输出功效}library(MASS)data(mcycle)attach(mcycle)windows(5,5) # 非参数的功效一般是通过绘图查察的plot(times,accel,xlab=”milliseconds”,ylab=”acceleration”)hs<-c(1,2,3,4) # 选择差异窗宽举办预计for(i in hs){ h=hs[i] fit<-lprq(times,accel,h=h,tau=0.5) # 要害拟合函数 lines(fit$xx,fit$fv,lty=i)}legend(45,-70,c(“h=1″,”h=2″,”h=3″,”h=4”), lty=1:length(hs)) |
功效：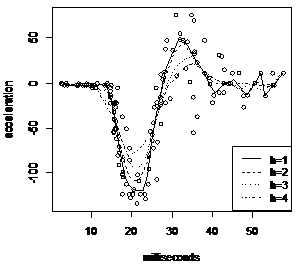
图2.6 基于正态漫衍为核函数的非参数拟合功效
| # 2-7-3 非参数回归的另一个要领—-# 考查较大的跑步速度与体重的干系data(Mammals)attach(Mammals)x<-log(weight) # 取得自变量的值y<-log(speed) # 取得因变量的值plot(x,y,xlab=”Weightinlog(Kg)”,ylab=”Speedinlog(Km/hour)”, type=”n”)points(x[hoppers],y[hoppers],pch=”h”,col=”red”)points(x[specials],y[specials],pch=”s”,col=”blue”)others<-(!hoppers&!specials)points(x[others],y[others],col=”black”,cex=0.75)fit<-rqss(y~qss(x,lambda=1),tau=0.9) # 要害的拟合步调plot(fit,add=T) # add=T暗示在上图中添加这里的曲线 |
功效：
图2.7 90%分位点下的附加分位数回归拟合功效（八）分位数回归的解析
| # MM2005分位数解析的函数，改变参数可直接利用MM2005 = function(formu,taus, data, group, pic=F){ # furmu 为方程，如foodexp~income # taus 为差异的分位数 # data 总的数据集 # group 分组指标，是一个向量，用于按行区分data # pic 是否绘图，假如分位数较量多，发起不绘图 engel1 = data[group==1,] engel2 = data[group==2,] # 开始举办解析 fita = summary( rq(formu, tau = taus, data = engel1 ) ) fitb = summary( rq(formu, tau = taus, data = engel2 ) ) tab = matrix(0,length(taus),4) colnames(tab) = c(“分位数”,”总差别”,”回报影响”,”变量影响”) rownames(tab) = rep(“”,dim(tab)[1]) for( i in 1:length(taus) ){ ya = cbind(1,engel1[,names(engel1)!=formu[[2]]] ) %*% fita[[i]]$coef[,1] yb = cbind(1,engel2[,names(engel2)!=formu[[2]]] ) %*% fitb[[i]]$coef[,1] # 这里以group==1为基准模子，用group==2的数据计较反通例模子拟合值 ystar = cbind(1,engel2[,names(engel2)!=formu[[2]]] ) %*% fita[[i]]$coef[,1] ya = mean(ya) yb = mean(yb) ystar = mean(ystar) tab[i,1] = fita[[i]]$tau tab[i,2] = yb – ya tab[i,3] = yb – ystar # 回报影响，数据沟通，模子差异：模子机制的差异所发生的差别 tab[i,4] = ystar – ya # 变量影响，数据差异，模子沟通：样本点差异发生的差别 } # 绘图 if( pic ){ attach(engel) windows(5,5) plot(income, foodexp, cex=0.5, type=”n”,main=”两组分位数回归功效较量”) points(engel1, cex=0.5, col=2) points(engel2, cex=0.5, col=3) for( i in 1:length(taus) ){ abline( fita[[i]], col=2 ) abline( fitb[[i]], col=3 ) } detach(engel) } # 输出功效 tab}# 下面是用一个样本数据做的测试data(engel)group = c(rep(1,100),rep(2,135)) # 取前100个为第一组，后135个第二组taus = c(0.05,0.25,0.5,0.75,0.95) # 需要考查的差异分位点MM2005(foodexp~income, taus, data = engel, group=group, pic=F) # 参数说明，见① |
说明：① 自编函数MM2005的参数说明：函数挪用形式MM2005 (formu, taus, data, group, pic=F)，个中
# furmu 为回归方程，如foodexp~income； # taus 为差异的分位数，如taus=c(0.05,0.5,0.95)； # data 总的数据集，如上例中的engel数据集； # group 分组指标，是一个向量，用于按行区分data，第一组为1，第二组为2；今朝仅能分两组；
# pic 逻辑参数：是否绘图。假如分位数较量多，发起不绘图；默认不绘图，pic=F；假如想绘图，则添加参数pic=T。② 最终功效：
> MM2005(foodexp~income, taus, data = engel, group=group, pic=F)
分位数 总差别 回报影响 变量影响
0.05 -30.452061 -72.35939 41.90733
0.25 -2.017317 -46.20125 44.18394
0.50 30.941212 -23.24042 54.18163
0.75 43.729025 -15.76283 59.49185
0.95 52.778985 -11.29932 64.07830
关键字：
