用nls函数举办非线性回归

在很多实际问题中，回归模子中响应变量和预测变量之间的干系大概是巨大的非线性函数。有时候能通过变量调动的要领可以将其变为线性模子，有时则不能。在后一种环境下，就需要采纳专门的非线性回归要领来成立模子。

非线性回归是在对变量的非线性干系有必然认识前提下，对非线性函数的参数举办最优化的进程，最优化后的参数会使得模子的RSS（残差平方和）到达最小。在R语言中更为常用的非线性回归建模函数是nls，下面以car包中的USPop数据集为例来讲授其用法。数据中population暗示人口数，year暗示年份。假如将二者绘制散点图可以发明它们之间的非线性干系。在成立非线性回归模子时需要事先确定两件事，一个长短线性函数形式，另一个是参数初始值。


一、模子拟合
对付人口模子可以回收Logistic增长函数形式，它思量了初期的指数增长以及总资源的限制。其函数形式如下。

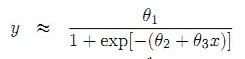
首先载入car包以便读取数据，然后利用nls函数举办建模，个中theta1、theta2、theta3暗示三个待预计参数，start配置了参数初始值，设定trace为真以显示迭代进程。nls函数默认回收Gauss-Newton要领寻找极值，迭代进程中第一列为RSS值，后头三列是各参数预计值。然后用summary返回回归功效。

library(car)

pop.mod1 <- nls(population ~ theta1/(1+exp(-(theta2+theta3*year))),start=list(theta1 = 400, theta2 = -49, theta3 = 0.025), data=USPop, trace=T)

summary(pop.mod)

在上面的回归进程中我们直接指定参数初始值，另一种要领是回收搜索计策，首先确定参数取值范畴，然后操作nls2包的暴力要领来获得最优参数。但这种要领相当费时。

尚有一种更为轻便的要领就是回收内置自启动模子(self-starting Models)，此时我们只需要指定函数形式，而不需要指定参数初始值。本例的logistic函数所对应的selfstarting函数名为SSlogis

pop.mod2 <- nls(population ~ SSlogis(year,phi1,phi2,phi3),data=USPop)

二、判定拟合结果
非线性回归模子成立后需要判定拟合结果，因为有时候参数最优化进程会捕获到局部极值点而非全局极值点。最直观的要领是在原始数据点上绘制拟合曲线。
library(ggplot2)

p <- ggplot(USPop,aes(year, population))

p+geom_point(size=3)+geom_line(aes(year,fitted(pop.mod1)),col=’red’)

若较量多个模子的拟合结果可利用AIC函数，取最小值为佳。

三、残差诊断
和线性回归雷同，非线性回归假设误差是正态、独立和同方差性。为了检测这些假设是否创立我们用拟合模子的残差来取代误差举办判定。

plot(fitted(pop.mod1) , resid(pop.mod1),type=’b’)

同方差假设回收残差值和拟合值的散点图判定，或是利用bartlett.test函数检测。正态性检测除了画QQ图外还可用shapiro.test函数。独立性检讨则可以绘制滞后残差图或是利用acf函数。

其它可以利用的泛型函数还包罗了anova、coef、confint、deviance、fitted、plot、predict、vcov。假如预测变量中包罗了分类数据，这种环境下可操作nlme包中的nlsList函数举办非线性回归。nlstools包中也有很多对非线性回归有用的函数。