用R语言举办分位数回归 第四节
这里利用某年份流感人口中小我私家消费和小我私家收入的数据作为案例，举办整体性阐明。（一）初始化措施
基本数据是dta名目（stata软件的数据名目），所以要用foreign包里的read.dta函数读取。这部门的主要内容包罗：
1、修改事情目次至措施和数据地址文件夹，留意不能利用“\”，必需利用“/”或“\\”；
2、排除其他变量、清理内存；
3、加载分位数回归所需的包quantreg和导入数据所需的foreign包；
4、加载4-functions.R文件中的R措施，这里有三个有用的函数；
5、读取案例数据20121218.dta；
6、初始化处理惩罚：去掉含有缺失值的行，查抄样本个数，查抄列名，整理列名，举办对数调动并生成新的数据集dat2。
| # 一个案例setwd(“F:/实践2/2012_分位数回归等两个任务/分位数回归要领夹”) # 配置事情目次setwd(””)rm(list=ls())gc()library(quantreg)library(foreign)source(“4-functions.R”) # 将4-functions.R中的函数放入内存中dat = read.dta(“20121218.dta”)dat = na.omit(dat) # 去掉有缺失值的行dim(dat) # 这个数据包括10000个样本，3个指标names(dat)# [1] “urtype” “q413” “q410a”# q413 每月家庭总收入# q410a 家庭食品支出# urtype 样本范例，1农村或2城镇# 这里考查上个月的收入与食品支出的干系，并分性别举办接头# 把变量的名称改一下names(dat) = c(“urtype”,”income”,”foodexp”)# 举办log调动dat2 = dat[dat$income>0 & dat$foodexp>0,]dat2[,”lnincome”] = log( dat2[,”income”] )dat2[,”lnfoodexp”] = log( dat2[,”foodexp”] )dat2 = na.omit(dat2) # 去掉log调动今后的缺失值行dim(dat2) |
（二）画散点图 画散点图的主要目标是查抄数据的漫衍是否需要举办对数调动，别的查察一下利用什么样的模子更符合。本案例中举办对数调动是要符合一些。
| # 散点图，调查是否需要log调动attach(dat)windows(5,5)# 稳定更plot(income,foodexp,cex=0.5,main=”散点图”)detach(dat)# 调动attach(dat2)windows(5,5)plot(lnincome,lnfoodexp,cexp=0.5,main=”散点图（对数调动今后）”)detach(dat2) |
功效：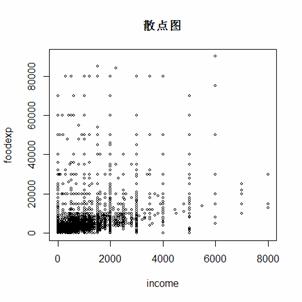
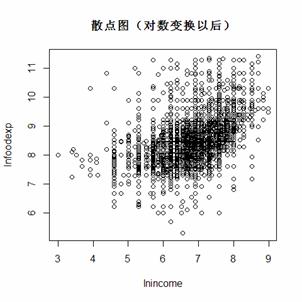图3.1 举办对数调动或差池数调动下的散点图（三）分位数回归的参数预计功效
挪用rq函数举办分位数回归预计。
1、这里选取的分位点包罗0.05、0.25、0.5、0.75和0.9。别离对整体数据、城镇和农村别离建模。假如数据量较大，发起method参数为“fn”或“pfn”，运算效率会高些。
2、用summary()函数可以获得越发具体的统计功效。
3、用笔者编写的tabs()函数和tabcoef()函数可以把summary()处理惩罚过的功效举办整合。留意，笔者的这两个函数在4-funcitons.R中，只有加载了这个文件（source(“4-functions.R”)）才气利用这两个函数，
| # 成立基本的分位数回归模子taus = c(0.05,0.25,0.5,0.75,0.95)fit1 = rq( lnfoodexp ~ lnincome, data=dat2, tau=taus, method=”fn” )fit2 = rq( lnfoodexp ~ lnincome, data=dat2[dat2$urtype==1,], tau=taus, method=”fn” )fit3 = rq( lnfoodexp ~ lnincome, data=dat2[dat2$urtype==2,], tau=taus, method=”fn” )# 所有数据放在一起是参数功效s1 = summary(fit1)# 男性s2 = summary(fit2)# 女性s3 = summary(fit3)# 参数功效的直接较量tabs(s1) # 这里的tabs函数是笔者本身写的，利便显示功效tabs(s2)tabs(s3)# 详细的系数预计值及假设检讨tabcoef(s1) # 这里的tabcoef函数是笔者本身写的，利便显示功效tabcoef(s2)tabcoef(s3) |
功效：表3-1-a 整体数据在差异分位点的系数（tabs(s1)）
| Quantiles | (Intercept) | lnincome |
| 0.05 | 4.26 | 0.50 |
| 0.25 | 4.55 | 0.52 |
| 0.50 | 5.01 | 0.50 |
| 0.75 | 5.43 | 0.49 |
| 0.95 | 5.93 | 0.52 |
表3-1-b 农村在差异分位点的系数（tabs(s2)）
| Quantiles | (Intercept) | lnincome |
| 0.05 | 3.69 | 0.58 |
| 0.25 | 4.31 | 0.55 |
| 0.50 | 4.69 | 0.55 |
| 0.75 | 5.01 | 0.55 |
| 0.95 | 5.59 | 0.58 |
表3-1-c 城镇在差异分位点的系数（tabs(s3)）
| Quantiles | (Intercept) | lnincome |
| 0.05 | 4.72 | 0.42 |
| 0.25 | 5.33 | 0.40 |
| 0.50 | 5.92 | 0.35 |
| 0.75 | 6.70 | 0.28 |
| 0.95 | 7.08 | 0.32 |
表3-1-d 整体在差异分位点的系数及其检讨功效（tabcoef(s1)）
| Quantiles | Value | Std. Error | t value | Pr(>|t|) |
| 0.05 | 4.26 | 0.093 | 45.869 | 0.000 |
| 0.05 | 0.50 | 0.014 | 36.819 | 0.000 |
| 0.25 | 4.55 |
关键字： |