R语言与函数预计进修条记（样条要领）

样条预计

假如函数在差异处所有差异的非线性度，可能有多个极值点，那么用多项式出格是低阶多项式来完成拟合长短常不符合的。一种办理步伐是我们之前提到的近邻多项式（可能称局部多项式），另一种就是样条——用分段的低阶多项式迫近函数。
关于样条，常用的有两类，一类是多项式样条，另一类是平滑样条。

多项式样条

多项式样条的样条基有许多，更为著名的是我们之前在函数迫近中提到的truncated power basis与B-spline basis。我们这里十分扼要的先容一下B样条，B样条基下的函数迫近可以写为：[ f(x)=beta_0+beta_1 x+cdots+beta_p x^p+sum_{j=1}^n beta_j B_j^p(x) ]个中[ B_i^p(x)=frac{x-c_i}{c_{i+p}-c_i}B_{i}^{p-1}(x)+frac{c_{i+p+1}-x}{c_{i+p+1}-c_{i+1}}B_{i+1}^{p-1}(x) ]上式中( B_i^0(x) =1 )当且仅当( c_i le x<c_{i+1} )不然取0.在R中splines包的函数bs()提供了B样条预计，其挪用名目为：

bs(x, df = NULL, knots = NULL, degree = 3, intercept = FALSE, Boundary.knots = range(x))

对付参数df值得说明的是df=degree+（Knots个数），attr(,“knots”)会显示分别点，我们常用的3次B样条公式: df=k+3 (不含常数项)
我们以前面提到的essay data为例说明B样条的预计环境：

easy <- read.table("D:/R/data/easysmooth.dat", header = T)
x <- easy$X
y <- easy$Y
m.bsp <- lm(y ~ bs(x, df = 6))


s = function(x) {
    (x^3) * sin((x + 3.4)/2)
}
x.plot = seq(min(x), max(x), length.out = 1000)
y.plot = s(x.plot)
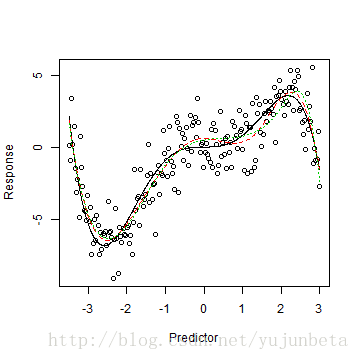
plot(x, y, xlab = "Predictor", ylab = "Response")
lines(x.plot, y.plot, lty = 1, col = 1)
lines(x, fitted(m.bsp), lty = 2, col = 2)

attr(bs(x, df = 6), "knots")  #可以将看到，节点在不指定的环境下默认的是匀称样条，虽然，我们可以按照散点图给#出节点的详细选择。

##    25%    50%    75% 
## -1.875 -0.250  1.375

m.bsp1 <- lm(y ~ bs(x, df = 6, knots = c(-2.5, -1, 2)))
lines(x, fitted(m.bsp1), lty = 3, col = 3)

AIC(m.bsp)

## [1] 718.1

AIC(m.bsp1)

## [1] 727.4

summary(m.bsp)

## 
## Call:
## lm(formula = y ~ bs(x, df = 6))
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -3.790 -0.911 -0.065  0.892  4.445 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)       1.816      0.622    2.92   0.0039 ** 
## bs(x, df = 6)1  -10.552      1.161   -9.09  < 2e-16 ***
## bs(x, df = 6)2   -7.127      0.755   -9.44  < 2e-16 ***
## bs(x, df = 6)3    0.813      0.926    0.88   0.3808    
## bs(x, df = 6)4   -4.056      0.859   -4.72  4.5e-06 ***
## bs(x, df = 6)5    5.781      0.967    5.98  1.1e-08 ***
## bs(x, df = 6)6   -3.505      0.865   -4.05  7.4e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.42 on 193 degrees of freedom
## Multiple R-squared:  0.824,  Adjusted R-squared:  0.819 
## F-statistic:  151 on 6 and 193 DF,  p-value: <2e-16

可以看到B样条根基很靠近真实函数了，summary(m.bsp)陈诉了各个系数的预计，带入( f(x) )的B样条基展开中即可获得一个显式的表达式。

平滑样条

固然B样条已经很好了，可是理论与实践都表白直接用最小二乘去求解系数结果欠好，容易过拟合。一个大概的改造是平滑样条。所谓的平滑样条，就是在求解最小二乘时给预计函数( f(x) )加上了必然的处罚，这个有点雷同压缩预计。我们这里回收最常用的平滑性处罚，获得函数( f(x) )的预计( m(x) )满意如下的处罚最小二乘：[ min sum_{i=1}^n (y_i-m(x_i))^2+lambda int [m”(x)]^2 dx ]在R的splines包中提供了函数smooth.spline来求解平滑样条

easy <- read.table("D:/R/data/easysmooth.dat", header = T)
x <- easy$X
y <- easy$Y
s.hat <- smooth.spline(x, y)

## OUTPUT
s.hat

## Call:
## smooth.spline(x = x, y = y)
## 
## Smoothing Parameter  spar= 0.7251  lambda= 0.0002543 (12 iterations)
## Equivalent Degrees of Freedom (Df): 11.56
## Penalized Criterion: 380.9
## GCV: 2.145

## OUTPUT PLOTS
s <- function(x) {
    (x^3) * sin((x + 3.4)/2)
}
x.plot = seq(min(x), max(x), length.out = 1000)
y.plot = s(x.plot)
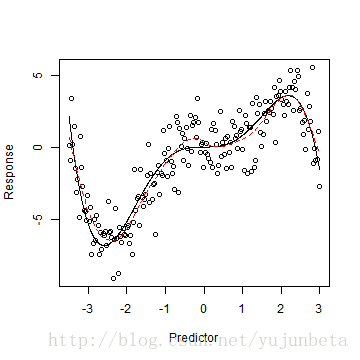
plot(x, y, xlab = "Predictor", ylab = "Response")
lines(x.plot, y.plot, lty = 1, col = 1)
lines(s.hat, lty = 2, col = 2)

#p#分页标题#e#

最后我们来讲一下怎么计较出( m(x) ),这里我们利用Reinsch algorithm。Step 1: 计较向量( Q’y ) .Step 2: 找到一个非0对角阵( R+lambda Q’Q ) 使得它可以举办Cholesky解析，有因子L，DStep 3: 解方程：( (R+lambda Q’Q)gamma=Q’y )Step 4: 获得估值( m=y-alpha Q gamma ).上面的Q与R可以暗示为：

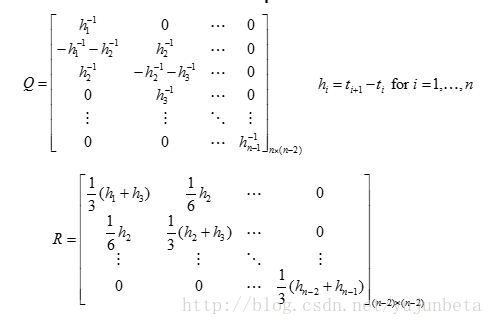
上面的t暗示节点。我们不妨来算算essay data的例子：

easy <- read.table("D:/R/data/easysmooth.dat", header = T)
x <- easy$X
y <- easy$Y


n <- length(y)
knots <- seq(min(x), max(x), length = n + 1)
h <- knots[-1] - knots[-n]
Q <- matrix(0, n, n - 2)
R <- matrix(0, n - 2, n - 2)
for (i in 1:(n - 2)) {
    Q[i, i] = 1/h[i]
    Q[i + 1, i] = -1/h[i] - 1/h[i + 1]
    Q[i + 2, i] = 1/h[i + 1]
}
for (i in 2:(n - 2)) {
    R[i, i] = 1/6 * (h[i] + h[i + 1])
    R[i - 1, i] = h[i]/6
    R[i, i - 1] = h[i]/6
}
R[1, 1] = 1/6 * (h[1] + h[2])
lambda <- 0.2
A <- R + lambda * t(Q) %*% Q
gamma <- solve(A, t(Q) %*% as.matrix(y))

g <- as.matrix(y) - lambda * Q %*% gamma

s <- function(x) {
    (x^3) * sin((x + 3.4)/2)
}
x.plot <- seq(min(x), max(x), length.out = 1000)
y.plot <- s(x.plot)
plot(x, y, xlab = "Predictor", ylab = "Response")
lines(x.plot, y.plot, lty = 1, col = 1)
lines(x, g, lty = 2, col = 2)

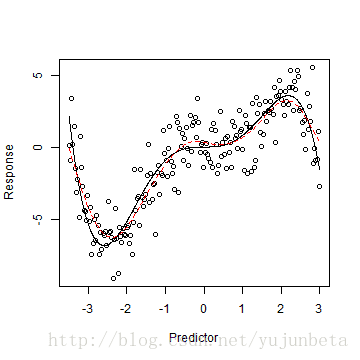
在处罚系数为0.2的环境下，拟合照旧不坏的，不是吗？至于为什么可以这样算，我们只要留意到( int [m^{”}(x)]dx=m^'(x_i)QR^{-1}Q^’m(x_i) ),预计的问题就与我们十分熟悉的lasso，岭回归十分相像了。