用Python中的LSTM进行股市预测|原创代码翻译
用Python中的LSTM进行股市预测
在Python中发现长期短期记忆(LSTM)网络,以及如何使用它们进行股市预测!
在本教程中,您将看到如何使用称为Long Short-Term Memory的时间序列模型。LSTM模型功能强大,特别是通过设计保留长期记忆,正如您稍后将看到的。您将在本教程中解决以下主题:
-
了解为什么你需要能够预测股票价格走势;
-
下载数据 – 您将使用从雅虎财经收集的股票市场数据;
-
分割列车测试数据并执行一些数据标准化;
-
重新审视并应用一些可用于提前一步预测的平均技术 ;
-
激励并简要讨论LSTM模型,因为它可以预测超过一步;
-
用当前数据预测未来股市并对其进行可视化
如果您不熟悉深度学习或神经网络,请参阅我们的Python深度学习课程。它涵盖了基本知识,以及如何在Keras中自行构建神经网络。这是一个与TensorFlow不同的包,它将在本教程中使用,但这个想法是一样的。
为什么你需要时间序列模型?
你想正确地模拟股票价格,所以作为一个股票买家,你可以合理地决定什么时候买股票,什么时候卖出来赚取利润。这就是时间序列建模的地方。您需要良好的机器学习模型,可以查看数据序列的历史记录,并正确预测序列的未来要素。
警告:股票市场价格非常不可预测且波动很大。这意味着数据中没有一致的模式,可以让您随时间对股价进行近似完美的模拟。不要把它从我这里拿出来,从普林斯顿大学经济学家Burton Malkiel那里拿出来,他在1973年的一本书“随意走下华尔街”中写道,如果市场真的有效率并且股价立即反映所有因素当他们被公开时,被蒙住眼睛的猴子在报纸上市投掷飞镖应该和任何投资专家一样好。
但是,我们不要一直认为这只是一个随机或随机过程,并且机器学习没有希望。让我们看看您是否至少可以对数据进行建模,以便您进行的预测与数据的实际行为相关联。换句话说,你不需要未来的确切股票价值,但股票价格变动(即,如果它在不久的将来会上涨)。
# Make sure that you have all these libaries available to run the code successfullyfrom pandas_datareader import dataimport matplotlib.pyplot as pltimport pandas as pdimport datetime as dtimport urllib.request, jsonimport osimport numpy as npimport tensorflow as tf # This code has been tested with TensorFlow 1.6from sklearn.preprocessing import MinMaxScaler
下载数据
您将使用以下来源的数据:
-
Alpha Vantage。然而,在你开始之前,你首先需要一个API密钥,你可以在这里免费获得。之后,您可以将该键分配给
api_key变量。 -
使用此页面中的数据。您需要将zip文件中的Stocks文件夹复制到项目主文件夹中。
股票价格有几种不同的风格。他们是,
-
开盘价:当天开盘价格
-
关闭:当天的收盘价格
-
高:数据的最高股价
-
低:当日最低股价
从Alphavantage获取数据
您将首先加载来自Alpha Vantage的数据。既然您要利用美国航空股票市场价格做出您的预测,您可以将股票价格设置为"AAL"。此外,您还定义了一个url_string,它将返回一个包含过去20年美国航空所有股票市场数据的JSON文件,以及一个file_to_save将保存数据的文件a 。您将使用ticker您事先定义的变量来帮助命名该文件。
接下来,您将指定一个条件:如果您尚未保存数据,则将继续并从您设置的URL中获取数据url_string; 您将日期,低,高,音量,关闭,开放值存储到熊猫数据框中,df然后将其保存到file_to_save。但是,如果数据已经存在,您只需从CSV中加载它。
从Kaggle获取数据
在Kaggle上发现的数据是csv文件的集合,您不必进行任何预处理,因此您可以直接将数据加载到Pandas DataFrame中。
data_source = 'kaggle' # alphavantage or kaggleif data_source == 'alphavantage':
# ====================== Loading Data from Alpha Vantage ==================================
api_key = ''
# American Airlines stock market prices
ticker = "AAL"
# JSON file with all the stock market data for AAL from the last 20 years
url_string = "https://www.alphavantage.co/query?function=TIME_SERIES_DAILY&symbol=%s&outputsize=full&apikey=%s"%(ticker,api_key)
# Save data to this file
file_to_save = 'stock_market_data-%s.csv'%ticker
# If you haven't already saved data,
# Go ahead and grab the data from the url
# And store date, low, high, volume, close, open values to a Pandas DataFrame
if not os.path.exists(file_to_save):
with urllib.request.urlopen(url_string) as url:
data = json.loads(url.read().decode())
# extract stock market data
data = data['Time Series (Daily)']
df = pd.DataFrame(columns=['Date','Low','High','Close','Open'])
for k,v in data.items():
date = dt.datetime.strptime(k, '%Y-%m-%d')
data_row = [date.date(),float(v['3. low']),float(v['2. high']),
float(v['4. close']),float(v['1. open'])]
df.loc[-1,:] = data_row
df.index = df.index + 1
print('Data saved to : %s'%file_to_save)
df.to_csv(file_to_save)
# If the data is already there, just load it from the CSV
else:
print('File already exists. Loading data from CSV')
df = pd.read_csv(file_to_save)else:
# ====================== Loading Data from Kaggle ==================================
# You will be using HP's data. Feel free to experiment with other data.
# But while doing so, be careful to have a large enough dataset and also pay attention to the data normalization
df = pd.read_csv(os.path.join('Stocks','hpq.us.txt'),delimiter=',',usecols=['Date','Open','High','Low','Close'])
print('Loaded data from the Kaggle repository')
Data saved to : stock_market_data-AAL.csv
数据探索
在这里,您将打印收集到DataFrame中的数据。您还应该确保数据按日期排序,因为数据顺序在时间序列建模中至关重要。
# Sort DataFrame by datedf = df.sort_values('Date')# Double check the resultdf.head()
| 日期 | 打开 | 高 | 低 | 关 | |
|---|---|---|---|---|---|
| 0 | 1970年1月2日 | 0.30627 | 0.30627 | 0.30627 | 0.30627 |
| 1 | 1970年1月5日 | 0.30627 | 0.31768 | 0.30627 | 0.31385 |
| 2 | 1970年1月6日 | 0.31385 | 0.31385 | 0.30996 | 0.30996 |
| 3 | 1970年1月7日 | 0.31385 | 0.31385 | 0.31385 | 0.31385 |
| 4 | 1970年1月8日 | 0.31385 | 0.31768 | 0.31385 | 0.31385 |
数据可视化
现在让我们看看你有什么样的数据。您希望随时间发生各种模式的数据。
plt.figure(figsize = (18,9))plt.plot(range(df.shape[0]),(df['Low']+df['High'])/2.0)plt.xticks(range(0,df.shape[0],500),df['Date'].loc[::500],rotation=45)plt.xlabel('Date',fontsize=18)plt.ylabel('Mid Price',fontsize=18)plt.show()
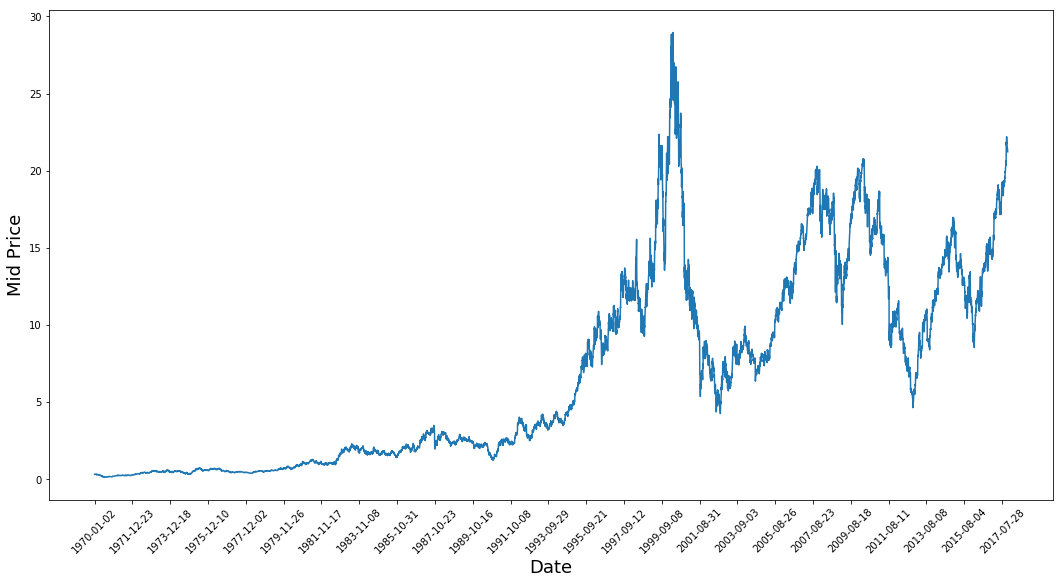
这张图已经说了很多东西。我选择这家公司的具体原因是这张图随着时间的推移出现了不同的股价行为。这将使学习更加强大,并给你一个改变,以测试对于各种情况的预测有多好。
另外需要注意的是,接近2017年的价格要高得多,并且比接近70年代的价格波动更大。因此,您需要确保数据在整个时间范围内的行为相似。在数据标准化阶段,你会处理这个问题。
将数据分成训练集和测试集
您将使用通过获取一天中最高和最低记录价格的平均值计算的中间价格。
# First calculate the mid prices from the highest and lowesthigh_prices = df.loc[:,'High'].as_matrix()low_prices = df.loc[:,'Low'].as_matrix()mid_prices = (high_prices+low_prices)/2.0
现在您可以分割训练数据和测试数据。训练数据将成为时间序列的前11,000个数据点,其余部分将成为测试数据。
train_data = mid_prices[:11000]test_data = mid_prices[11000:]
规范化数据
现在您需要定义一个缩放器来规范数据。MinMaxScalar将所有数据缩放到0和1的范围内。您还可以将训练和测试数据重塑为形状[data_size, num_features]。
# Scale the data to be between 0 and 1# When scaling remember! You normalize both test and train data with respect to training data# Because you are not supposed to have access to test datascaler = MinMaxScaler()train_data = train_data.reshape(-1,1)test_data = test_data.reshape(-1,1)
由于您之前所做的观察,即不同时间段的数据具有不同的值范围,因此您可以通过将整个系列分成多个窗口来标准化数据。如果您不这样做,则较早的数据将接近于0,并且不会为学习过程增加太多价值。在这里你选择一个2500的窗口大小。
提示:在选择窗口大小时,请确保窗口大小不要太小,因为当执行窗口规范化时,它可以在每个窗口的最后引入一个中断,因为每个窗口都是独立标准化的。
在这个例子中,4个数据点会受到这个影响。但是考虑到你有11,000个数据点,4点不会引起任何问题
# Train the Scaler with training data and smooth datasmoothing_window_size = 2500for di in range(0,10000,smoothing_window_size): scaler.fit(train_data[di:di+smoothing_window_size,:]) train_data[di:di+smoothing_window_size,:] = scaler.transform(train_data[di:di+smoothing_window_size,:])# You normalize the last bit of remaining datascaler.fit(train_data[di+smoothing_window_size:,:])train_data[di+smoothing_window_size:,:] = scaler.transform(train_data[di+smoothing_window_size:,:])
将数据重塑为形状 [data_size]
# Reshape both train and test datatrain_data = train_data.reshape(-1)# Normalize test datatest_data = scaler.transform(test_data).reshape(-1)
您现在可以使用指数移动平均数来平滑数据。这有助于您摆脱股票价格数据固有的不规则性并产生更平滑的曲线。
请注意,您只应该平滑训练数据。
# Now perform exponential moving average smoothing# So the data will have a smoother curve than the original ragged dataEMA = 0.0gamma = 0.1for ti in range(11000): EMA = gamma*train_data[ti] + (1-gamma)*EMA train_data[ti] = EMA# Used for visualization and test purposesall_mid_data = np.concatenate([train_data,test_data],axis=0)
通过求平均的一步预测
平均机制允许您通过将未来股票价格表示为先前观察到的股票价格的平均值来预测(通常是前一步)。这样做多于一个时间步骤可能会产生相当不好的结果。你会看到下面的两种平均技术。标准平均和指数移动平均。您将对两种算法产生的结果进行定性(视觉检测)和定量(均方差)评估。
均方误差(MSE)可以通过取前一步的真值与预测值之间的平方误差并在所有预测中求平均值来计算。
标准平均
您可以首先尝试将此模型作为平均计算问题进行建模,从而了解此问题的难度。首先,您将尝试将未来股票市场价格(例如x t +1)预测为在固定尺寸窗口内的先前观察到的股票市场价格的平均值(例如x t-N,…,x t)(说前100天)。此后,您将尝试更多更漂亮的“指数移动平均线”方法,并看看效果如何。然后你将进入时间序列预测的“圣杯”; 长期短期记忆模型。
首先你会看到正常的平均值是如何工作的。那是你说的,

换句话说,你说$ t + 1 $的预测值是你在$ t $到$ tN $窗口内观察到的所有股票价格的平均值。是在t到t–N窗口内观察到的所有股票价格的平均值。t+1tt−N
window_size = 100N = train_data.sizestd_avg_predictions = []std_avg_x = []mse_errors = []for pred_idx in range(window_size,N):
if pred_idx >= N:
date = dt.datetime.strptime(k, '%Y-%m-%d').date() + dt.timedelta(days=1)
else:
date = df.loc[pred_idx,'Date']
std_avg_predictions.append(np.mean(train_data[pred_idx-window_size:pred_idx]))
mse_errors.append((std_avg_predictions[-1]-train_data[pred_idx])**2)
std_avg_x.append(date)print('MSE error for standard averaging: %.5f'%(0.5*np.mean(mse_errors)))
MSE error for standard averaging: 0.00418
看看下面的平均结果。它紧密地跟踪股票的实际行为。接下来,您将看到更准确的一步预测方法。
plt.figure(figsize = (18,9))plt.plot(range(df.shape[0]),all_mid_data,color='b',label='True')plt.plot(range(window_size,N),std_avg_predictions,color='orange',label='Prediction')#plt.xticks(range(0,df.shape[0],50),df['Date'].loc[::50],rotation=45)plt.xlabel('Date')plt.ylabel('Mid Price')plt.legend(fontsize=18)plt.show()
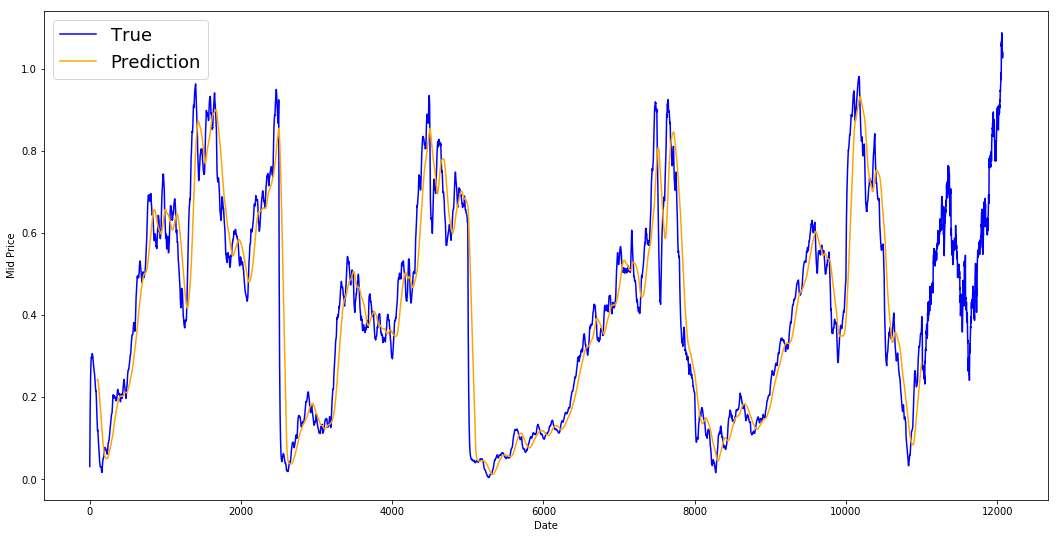
那么上面的图表(和MSE)会说什么?
对于非常短的预测来说,它似乎并不算太坏(前一天)。鉴于股价在一夜之间不会从0变为100,这种行为是明智的。接下来,您将看到一种称为指数移动平均值的发烧友平均技术。
指数移动平均线
您可能已经在互联网上看到了一些使用非常复杂的模型的文章,并几乎预测了股票市场的确切行为。但要小心!这些只是光学幻想,并不是因为学习有用的东西。您将在下面看到如何使用简单的平均方法来复制该行为。
在指数移动平均法中,您计算$ x_ {t + 1} $ as, as,xt+1
-
X t + 1的 = EMA 吨 =γ×EMA T-1 +(1-γ)x 吨,其中EMA 0 = 0和EMA是你保持随时间的指数移动平均值。
上面的等式基本上是从$ t + 1 $时间步计算出指数移动平均值,并将其用作一步预测。$ \ gamma $决定最近预测对EMA的贡献。例如,$ \ gamma = 0.1 $只能获得EMA当前值的10%。因为你只占最近的一小部分,所以它可以保留你在平均早期看到的更老的值。看看如何用它来预测下面的一步。时间步并将其用作一步预测。γ决定了最近预测对EMA的贡献。例如,γ=0.1只能得到EMA当前值的10%。因为你只占最近的一小部分,所以它可以保留你在平均早期看到的更老的值。看看如何用它来预测下面的一步。t+1γγ=0.1
window_size = 100N = train_data.sizerun_avg_predictions = []run_avg_x = []mse_errors = []running_mean = 0.0run_avg_predictions.append(running_mean)decay = 0.5for pred_idx in range(1,N):
running_mean = running_mean*decay + (1.0-decay)*train_data[pred_idx-1]
run_avg_predictions.append(running_mean)
mse_errors.append((run_avg_predictions[-1]-train_data[pred_idx])**2)
run_avg_x.append(date)print('MSE error for EMA averaging: %.5f'%(0.5*np.mean(mse_errors)))
MSE error for EMA averaging: 0.00003
plt.figure(figsize = (18,9))plt.plot(range(df.shape[0]),all_mid_data,color='b',label='True')plt.plot(range(0,N),run_avg_predictions,color='orange', label='Prediction')#plt.xticks(range(0,df.shape[0],50),df['Date'].loc[::50],rotation=45)plt.xlabel('Date')plt.ylabel('Mid Price')plt.legend(fontsize=18)plt.show()
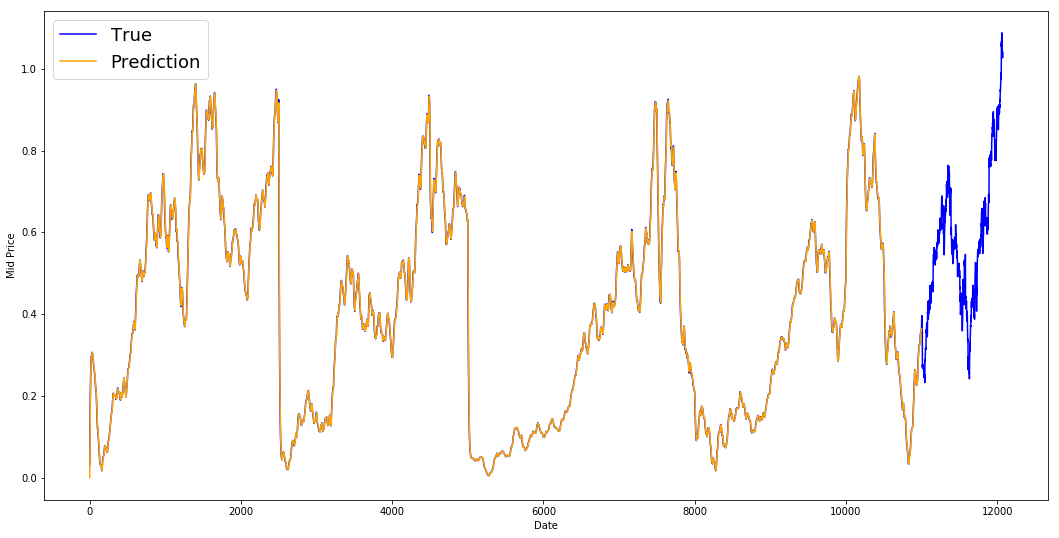
如果指数移动平均线很好,为什么你需要更好的模型?
你会发现它符合True分布之后的完美线条(并且由极低的MSE证明)。实际上,仅凭第二天的股票市值就无法做多。个人而言,我想要的不是第二天的确切股票市场价格,但是股票市场价格会在未来30天内上涨或下跌。试着这样做,你会暴露出EMA方法的不可用性。
您现在将尝试在窗口中进行预测(例如,您预测接下来的2天窗口,而不是第二天)。然后你会意识到EMA可能会出错。这里是一个例子:
预测未来一步
为了使事情具体,让我们假设值,例如$ x_t = 0.4 $,$ EMA = 0.5 $和$ \ gamma = 0.5 $xt=关键字:
