在J2ME/MIDP中实现图像旋转
副标题#e#
J2ME是尺度版java(J2SE)面向手机、PDA等种种移动和嵌入式设备的缩减版本,是一种得到浩瀚厂商的支持和遍及利用的移动设备开拓平台。图一展示了J2ME技能的体系布局。它分为三层:虚拟机层,设置层,和简表层。 设置层(Configuration)通过对成果的描写,把千差万此外嵌入式设备举办了成果的说明和分类。它把运算成果有限、内存较小、电力有限的设备,界说在CLDC(有限毗连设备设置)类型中,这类设备有PDA 、手机等;把运算本领相对较佳、内存相对较大、电力供给较量富裕的设备,界说在CDC(毗连设备设置)类型之中,这类设备有电冰箱、机顶盒、车载计较设备等。
虚拟机层(Virtual Machine)基于宿主操纵系统,凭据某一种设置,实现了Java虚拟机。CDC设置对应的虚拟机叫CVM,CLDC对应的虚拟机叫做KVM。
简表层(Profile)成立在设置层之上,提供了面向用户的更高条理的成果,如用户接口,网络,数据存储等。基本类型(Foundation Profile)和小我私家类型(Personal Profile)是CDC之上的两个重要的类型,移动信息设备类型(MIDP)和PDA类型(PDAP)是CLDC之上的两个重要的类型。当前,无线应用措施的开拓主要是在MIDP之长举办的。
设置层和简表层配合组成了J2ME的运行情况。如CLDC/MIDP架构构筑了手机应用措施的开拓和运行情况。本文所实现的图像旋转算法即是基于这种架构的。
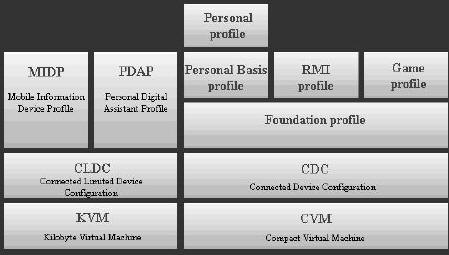
图一 J2ME 体系布局 需要留意的是,这些类型也是在不绝成长的。如早期许多的设备的计较本领很是有限,CLDC1.0就只支持整型数值。厥后数跟着设备运算本领的提高,CLDC1.0成长到CLDC1.1,就加如了对浮点运算的支持。对MIDP类型也一样,从1.0成长到2.0,它通过扩充类和接口的成果,增强了对游戏开拓的支持,增加了图像处理惩罚成果(旋转要用到),加强了对网络成果的支持,如串口、套接字、https等。
2D旋转的数据基本
思量笛卡儿直角坐标系中单个点旋转的环境。如图二示,这里点P(x,y)到原点O绕O点逆时针旋转角度θ后到点P′(x′,y′)。由三角函数的几许意义,有x = r*cos α ,y = r*si n α和x′ = r*cos(α +θ) , y′ = r*sin(α + θ),推出:
x′ = x * cos θ – y * sin θ
y′ = y * cos θ + x * sin θ
当把旋转点一般化为Q(x0,y0),获得:
x′ = x0 + (x – x0) cos θ – (y – y0) sin θ
y′ = y0 + (y – y0) cos θ + (x – x0) sin θ
在开拓时,我们利用设备坐标系,它以屏幕的左上角为坐标原点,y轴偏向向下。此时,我们不妨视θ为饶旋转点顺时针旋转的角度,这样,上面的公式依然创立。
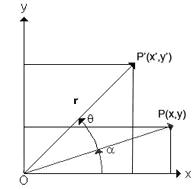
图二 2D点的旋转 一般图像的旋转算法
#p#副标题#e#
1、算法思想 为实现整个图像的旋转,我们首先获取源图像每个点的像素值。然后按照旋转点和角度的巨细计较出新图像的巨细。再逐点计较源图像中每个点经旋转后在新图像中对应点的坐标,并把相应的像素值赋给它。
在图三中,阴影部门为源图像,O为旋转点,P、Q别离为旋转前后图像左上角的点,cx,cy为O相对付源图像左上角P点的坐标值。
这里我们以O为圆心,以O距图像4个极点的间隔的最大值作为半径dr画圆,这样图像无论以任何角度旋转都不会超出这个圆的范畴。于是,我们就以该圆为画布绘制旋转所得新图像。由于实际中图像是用矩形暗示的,于是我们生成和圆的外切正方形(图中虚线部门)等巨细的新图像。
对源图像中任一点(i,j),按照上面的公式,不难计较出旋转θ度在新图像中的位置,即相对付Q点的位置(destX , destY):
destX = dr + (i – cx) *cos(radian) – (j – cy)*sin(radian);
destY = dr + (j – cy) *cos(radian) + (i – cx)*sin(radian);
计较出这个位置后,把该点的像素值赋值到这个位置,如此对每个点举办这种调动,即可实现整个图像的旋转。
旋转后的图像较大,在实际绘制时需要做位置调解,不丢脸出,Q点相对付P点的偏移量为(cx-dr , cy-dr)。即假设源图像的屏幕位置为(a , b),则旋转后的图像位置应该为( (a + cx – dr) , (b + cy – dr) )。
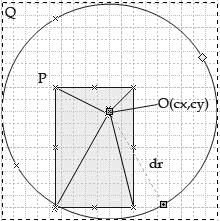
图三 旋转算法示意图 2、在J2ME中的算法实现
我们将上面的思想详细化,获得算法的流程图(见图四示)
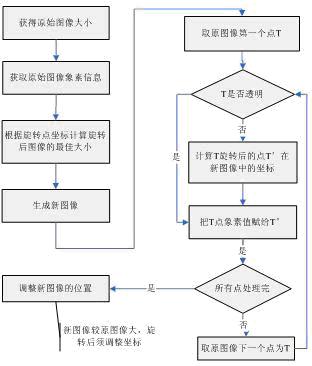
#p#分页标题#e#
图四 算法流程图 在MIDP2.0中,Image类提供了两个要领:getRGB()和createRGBImage(),别离完成获取图像象素信息和通过像素数组建设图像的成果。借助于这两个要领,团结上面的流程图,我们获得实现图像旋转算法的代码,如下面所示。 /**
*@param imgSource 源图像
*@param cx 旋转点相对付源图像坐上角横坐标
*@param cy 旋转点相对付源图像坐上角纵坐标
*@param theta 图像逆时针旋转的角度
*@param dd 含2个元素的整形数组,存放新图像相对源图像沿x轴和y轴的位置偏移量
*@return 旋转后的图像
**/
public Image rotate(Image imgSource, int cx, int cy, double theta, int[] dd) {
if (Math.abs(theta % 360) < 0.1) return imgSource; //角度很小时直接返回
int w1 = imgSource.getWidth(); //原始图像的高度和宽度
int h1 = imgSource.getHeight();
int[] srcMap = new int[w1 * h1];
imgSource.getRGB(srcMap, 0, w1, 0, 0, w1, h1); //获取原始图像的像素信息
int dx = cx > w1 / 2 ? cx : w1 – cx; //计较旋转半径
int dy = cy > h1 / 2 ? cy : h1 – cy;
double dr = Math.sqrt(dx * dx + dy * dy);
int wh2 = (int) (2 * dr + 1); //旋转后新图像为正方形,其边长+1是为了防备数组越界
int[] destMap = new int[wh2 * wh2]; //存放新图像象素的数组
double destX, destY;
double radian = theta * Math.PI / 180; //计较角度计较对应的弧度值
for (int i = 0; i < w1; i++) {
for (int j = 0; j < h1; j++) {
if (srcMap[j * w1 + i] >> 24 != 0) { //对非透明点才举办处理惩罚
// 获得当前点经旋转后相对付新图像左上角的坐标
destX = dr + (i – cx) * Math.cos(radian) + (j – cy)* Math.sin(radian);
destY = dr + (j – cy) * Math.cos(radian) – (i – cx)* Math.sin(radian);
//从源图像中往新图像中填充像素
destMap[(int) destY * wh2 + (int) destX] = srcMap[j * w1 + i];
}
}
}
dd[0] = cx-dr; //返回位置偏移分量
dd[1] = cy-dr;
return Image.createRGBImage(destMap, wh2, wh2, true); //返盘旋转后的图像
}
3、旋转失真问题 因为旋转公式含有三角函数,所以求出的旋转坐标取整后有大概插入到先前已插入的位置中,而没有插入到它本应该插入的位置。譬喻:计较出旋转坐标(3.1,4)取整后插入到(3,4)中;假如计较下个旋转坐标为(3.4,4),取整后又被插入到(3,4)中,因此包围了本来的像素点,并且(3.4,4)对应的像素点没有步伐插入到它应该插入的位置,造成失真。
要办理这个问题,在不思量牺牲特别资源的环境下,一般的要领是先将图像放大若干倍,然后再举办旋转,再等比例缩小。对付界线可思量马赛克的处理惩罚方法可能用两行重描赔偿误差的步伐。
算法的应用与范围性
1、模仿浮点运算
上述算法是基于cldc1.1类型的,该类型提供了对浮点运算和三角函数运算的直接支持。为提高措施的通用性,我们但愿算法能运行在cldc1.0设备上。
cldc1.0不支持任何非整形的数值,要实现三角函数的计较,我们可以思量用已有的整型数来模仿浮点数:把一个整数分成两个域,别离存放浮点的整数和小数部门,这并不难,但要模仿通用的数学函数,如正弦、余弦、二次方根、指数运算等就不那么容易了,需要耗费不少时间。由于一些现有的库已经可以或许很好地完成这些事情,一般环境下,我们可以直接拿来用。
这里我们选用Onne Hommes编写的MathFP库,该库提供了基于整形int和长整形long的差异精度的实现,有简朴、结实、速度快的特点。看下面利用该库的示例代码:
int xFP = MathFP.toFP(“0.10”);
int yFP = MathFP.toFP(“0.2”);
int zFP = MathFP.mul(xFP , yFP);
System.out.println( MathFP.toString( zFP ) ); //0.02
前两行结构了两个定点数0.10和0.2,第三行计较他们的乘积,并按照这个值结构定点数zFP,最后一行把zFP的值输出。
这些定点值xFP,yFP,zFP不是真正意义上的整型值,固然它们用整型值来存储数据。利用这些定点值时必需挪用相应的MathFP要领。
此外可以选用的浮点运算库有JMFP、FPLib、shiftFP等。
2、利用预置的三角函数表
三角函数的计较一般较量慢,为提高运行速度,我们可以对数值举办估量算,好比提前计较出360?以内角度的正弦和余弦值,把功效存储在一个静态数组中,如下面代码。
static int[] lookupCosFP = new int[360];
static int[] lookupSinFP = new int[360];
long radianFP ; //用于存放角度的弧度值
for(int i = 0; i<360; i++ ) {
//将角度转化为弧度,利用MathFP库
radianFP=MathFP.div(MathFP.mul(MathFP.toFP(i),MathFP.PI),MathFP.toFP(180)) ;
lookupCosFP = MathFP.cos(radianFP); //存入数组
lookupSinFP = MathFP.sin(radianFP);
}
#p#分页标题#e#
这样利用时,从数组中直接值就行了。事实上,按照三角函数的特点,我们只需估量算存储0-90度的正弦函数值,便可以导出任意角度的正弦、余弦值。读者可以编写一个单独的要领实现之。 由于移动设备的屏幕凡是较量小,做高精度的三角函数运算的意义不大,所以一般采纳近似模仿的步伐。(1)对有浮点支持/第三方库支持的环境,不去存放每个角度的三角函数值,每隔5?存一个值。(2) 对付没有浮点支持和第三方浮点库支持的环境,在表中存放角度的三角函数值乘以某个较大数(如4096)取整后的值,在实际计较之后,再等比例缩小(除以4096)。这两种要领在实际中都有不少应用。
3、Sprite中的图像旋转
Sprite,即精灵,是在游戏中代表脚色的类,它打点所有的图像帧来实现各类动画结果,在游戏开拓中有着遍及的应用。假如需要表示动画结果,那用Sprite是再符合不外的了。MIDP2.0中,提供了专门的这样一个类,在结构时只需把图像工具作为参数通报。Sprite类自身提供了图像反射和成90度整数倍旋转的成果。假如要实现任意角度旋转,本质上跟上面的Image的旋转没有别离,只是在Sprite中内置了精灵的位置等信息,打点起来会越发利便高效。
读者可以参考上面Image的实现,利便写出基于Sprite的旋转实现。需留意的是,Sprite一次只能取一帧图像,因此需要首先把该帧从图像会合提取出来。图五展示了“淘金者”游戏中,精灵类“钩子”的逆时针偏向0到60?的旋转结果图。

图五 钩子的旋转结果 4、范围性
(1)该算法的利用进程中生成了较大的图像,较量适合于图像绕牢靠点持续旋转环境。假如实际中图像只需做一次旋转,或旋转点常常调动,这种要了解发生较大的无效区域,增加处理惩罚的承担,此时,旋转后图像的巨细最好按照旋转点和角度做最优化计较。
(2)算法需要得到图像的象素信息,这在midp2.0才给以支持,假如要在midp1.0的呆板上实现图像旋转,须借助于设备厂商专用开拓包,如Nokia开拓包就提供了DirectUtils类实现雷同上面createRGBImage()的成果。虽然这只能在相应设备上才气用。
(3)算法要求设备支持Alpha通道,不然不能正常的表示结果。
(4)基于该要领的Sprite工具在做碰撞检测时,须回收象素检测的要领。
其余方案
1、预置图像
预置图像就是把所需要的各个角度的图像预先存储起来,然后按需直接挪用的要领。这种要领不需要我们在措施中做像素级的操纵,所以利用起来较简朴。缺点是当要存储的图像种别和角度很大时,会增加不少存储开销。
当所需要的各角度的图像为偶数个且在0-360?范畴内匀称漫衍时,借助于MIDP2.0的Sprite类提供的顺时针旋转90?、180?、270?度的成果,我们可以在必然水平上低落这种开销。好比在坦克大战游戏中,如果一辆坦克需要一周范畴内匀称漫衍的12个差异的偏向,则需预置12副图像。借助于该要领,只需要提供三张图片就够了(见图六),当它们别离旋转90?、180?和270?后就获得了完整的12个偏向,节减了3/4的存储开销。
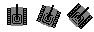
图六 预置图像
2、利用TinyLine 2D
这是一个用于高机能图形绘制的j2me开拓包。它面向措施员,界说了一组紧凑的2d图形工具集,扩展了j2me在移动设备上的图形表示本领。它提供了基于CLDC 1.0 纯Java语言的实现,很小巧,整个库不敷35k,可以或许很利便地集成到应用措施傍边去。需要说明的是,该库不单支持图形,对一般意义上的光栅图像也支持,通过它也能实现旋转等的操纵。
结论
J2ME作为移动信息设备上的开拓应用措施的开放平台,得到了浩瀚厂商的支持,和越来越遍及的利用。本文从数学的基本出发,提出了实现图像按任意角度旋转的一种方案并给出了基于J2ME/MIDP平台的实现,给出结范围性阐明,最后引出了实现图像旋转的别的两种参考性要领。其实要领并没有好劣之分,只有适合不适合之说,在实际应用中,我们应按照详细的需求,选择最符合的方案。但愿本文能给读者在J2ME开拓中需要用到图像旋转的成果时提供有益的参考
