Robocode根基道理之坐标锁定
当前位置：以往代写 > JAVA 教程 >Robocode根基道理之坐标锁定

Robocode根基道理之坐标锁定

2019-06-14

Robocode根基道理之坐标锁定

Robocode根基道理之坐标锁定

副标题#e#

导论

前面我们相识了Robocode中的绝对偏向，相对偏向及整个偏向系统。相信大 家对此深有体会了。可是问题又来了，单知道偏向好像不能完全到达相识仇人的 目标。奈何去探测仇人的间隔？奈何准确的锁定方针呢？对付移动中的方针我们 又如那里理惩罚?在这里我们将操作Java.lang 根基类库中的Math类及一些根基三角 函数要领为你揭开这些迷雾。对付那些快被遗忘的三角几许常识在本文的最后 Skyala.Li有较量具体的讲授。

坐标根基观念

首先我们照旧来看看Robocode API中的一段文字翻译。

All coordinates are expressed as (x,y).

所有的坐标都用x,y来暗示

All coordinates are positive.

所有的坐标都为正

The origin (0,0) is at the bottom left of the screen.

坐标原点(0,0)在屏幕的左下角

Positive x is right. X的右边为正

Positive y is up. Y的上面为正

图1显示了Robocode中的坐标系统，有关图的具体说明请看我们前面先容的文 章 “Robocode根基道理之偏向分解”.

图1

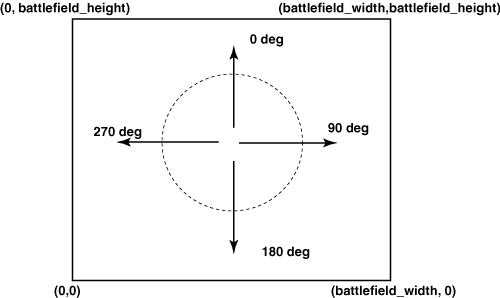
Robocode根本原理之坐标锁定


#p#副标题#e#

“消息呆板人”测试法

好了，我们知道了Robocode整个坐标系统，一切问题都好办了。先让我们进 行一些有趣的尝试。我们仍以”消息呆板人”的要领举办测试。这是个测试呆板 人偏向，坐标参数的很好步伐。见下说明：

设计两个呆板人，任意取名为Geny和GenyTrack。Geny是个静止的呆板人，它 主要任务是打印本身的当前坐标，用来验证GenyTrack追踪它的位置是否正确。 GenyTrack顾名思义，它就是我们要研究的追踪方针呆板人了。它在此认真锁定 Geny的坐标，间隔并打印出探测到的Geny呆板人的X,Y坐标及间隔,此处利用了 Java.lang类库中的Math.round要领,四舍五入获得的double范例的数据，利便对 比。最后用表格比拟，以此来验证我们利用要领的正确性。

虽然尚有许多有趣的测试要领来期待着你的验证。如测速度，加快度时我们 就可用”龟兔赛跑”的要领；测炮管，雷达坦克车旋转彼此影响度可用”离心重 力”的要领。相信从测试要领的名字智慧的你们就知道他的用法了。

在我们开始前，Skyala.Li发起你们下载源码( resource)先看看GenyTrack的 演出。虽然你也可参考文章内附加的帮助说明Robocode坐标系统的代码。

Geny:
package　test;
import　robocode.*;
public　class　Geny　extends　AdvancedRobot
{
　　 public　void　run　()
　　 {
　　　　 while　(true)
　　　　 {
　　　　　　 //　round　对get到的数据举办四舍五入处理惩罚
　　　　　　 out.println("x:"+Math.round(getX()));
　　　　　　 out.println("y:"+Math.round(getY()));
　　　　 }
　　 }
}

GenyTrack:

package　test;
import　robocode.*;

public　class　GenyTrack　extends　AdvancedRobot
{
　　 public　void　run　()
　　 {
　　　　 while　(true)
　　　　 {
　　　　　　 turnRadarRight(400);
　　　　 }
　　 }
　　 public　void　onScannedRobot(ScannedRobotEvent　e)
　　 {
　　　　 double　bearing　=　(getHeading()　+　e.getBearing())　%　 360;
　　　　 double　distance　=　e.getDistance();
　　　　 bearing　=　Math.toRadians(bearing);

　　　　 double　genyX　=　getX()　+　Math.sin(bearing)　*　 distance;
　　　　 double　genyY　=　getY()　+　Math.cos(bearing)　*　 distance;

　　　　 out.println("genyX:"+　Math.round(genyX));
　　　　 out.println("genyY:"+　Math.round(genyY));
　　 }
　 }

留意这两个呆板人我们都利用了AdvancedRobot的类，这但是高级呆板人的说 明白。有关高级呆板人各人可以查找Robocode API的说明，也可看看Sing Li的 "Rock ’em, sock ’em Robocode: Round 2".

#p#副标题#e#

间隔探测

要获得方针坐标我们首先得知道我们和方针之间的间隔。这里的间隔探测很 简朴，只要运用GenyTrack呆板人ScannedRobotEvent事件中的 getDistance()方 法我们就可获得Geny呆板人和你之间的间隔差了。只是要留意一点，由于呆板人 存在着宽和高,可别离用Robocode API 中的getWidth()和getHeigth()要领获得 。而两个呆板人的间隔是以两边的中心点为终点。如图所示，L才是它们的间隔 ，A的间隔是错误的。

图2

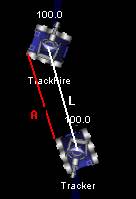
Robocode根本原理之坐标锁定

坐标探测

知道了对方的间隔，知道了整个坐标系统。我们就来锁定我们的方针Geny.我 们先来看看图3所示：

图3

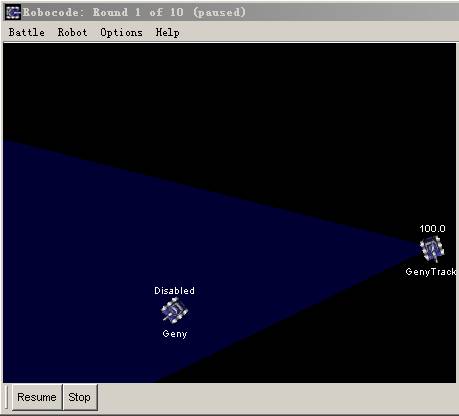
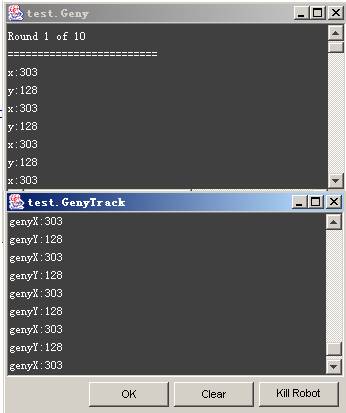
Robocode根本原理之坐标锁定

Robocode根本原理之坐标锁定

#p#副标题#e#

列表1：

#p#分页标题#e#

Geny GenyTrack
X:303 genyX:303
Y:128 genyY:128

列表1就是我们用”消息呆板人”测试法得出的数据。你将会惊喜若狂，不错 ，我们乐成的探测到了我们可怜的Geny的坐标。惊喜事后你就会不大白了:我们 是奈何实现这一切的？为什么代码中利用到了非Robocode中的类库Math，还好像 用到了正余弦求解，尚有弧度？不错，这就是Robocode:随处都让我们诧异，处 处都让我们进修新的常识。假如你对中学时代的数学三角几许解法已经生疏，没 干系，你将在我们本文最后的 三角函数基本中将进修到这些。它将勾起你中学 时代的影象。

此刻让我们来阐明阐明我们GenyTrack到底做了些什么：

在 GenyTrack的ScanndeRobotEvent事件中我们首先获得Geny的绝对角度 bearing，也即相对屏幕的角度。并从 ScannedRobotEvent扫描事件中获得的大 量信息阐明中提炼出Geny和GenyTrack的间隔为distance。有了Geny的角度, 有 了Geny的间隔我们再按照三角学基本（详见文 三角函数基本）就可求出Geny的 准确坐标了。

又由于Java类库中的正弦函数sin余弦函数cos是以弧度制（详见文 三角函数 基本）为角度的参数。所以我们操作了Math.toRadians要领把Geny的绝对角度转 化为弧度。见列表2

列表2：

double　bearing　=　(getHeading()　+　e.getBearing ())　%　360;
　　　　 double　distance　=　e.getDistance();
　　　　 bearing　=　Math.toRadians(bearing);

　　　　 double　genyX　=　getX()　+　Math.sin(bearing)　*　 distance;
　　　　 double　genyY　=　getY()　+　Math.cos(bearing)　*　 distance;

　　　　 out.println("genyX:"+　Math.round(genyX));
　　　　 out.println("genyY:"+　Math.round(genyY));

留意三角函数的基本中：对边长=sina *斜边长，侧边长=cosa＊斜边长，但 要记着Robocode中三角坐标系统中的sin和cos和我们数学中的三角坐标系统有一 定不同，也即上面的 sina和cosa要对调，对边长=cosa*斜边长。图4画出了Geny 和GenyTrack之间角度和间隔的干系以及Robocode所回收的三角坐标系统。

图4

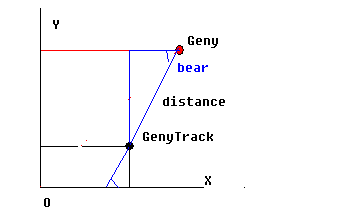
Robocode根本原理之坐标锁定

黑线条为GenyTrack的X，Y坐标,蓝线条以Geny的间隔distance和绝对角度 bear求得的X,Y坐标,两者相加获得的就是Geny的X和Y坐标。

至于Math类库的利用，我们就不具体说明白。读者也可从下面的IBM Java专 区链接中找到许多有关的常识，也可参考一些Java类库书籍说明。当你设计高级 Robocode呆板人时你会发明，Math类库是你不行缺少的一部门常识。此处我们只 简朴的先容正弦函数及余弦函数的利用。

Sin
public　static　double　sin(double　a)
Returns　the　trigonometric　sine　of　an　angle.
Parameters:
a　-　an　angle,　in　radians.
Returns:
the　sine　of　the　argument

Sin函数返回三角的正弦函数，参数a是一个以double范例以弧度暗示的角度 值，返回范例为double.

cos
public　static　double　cos(double　a)
Returns　the　trigonometric　cosine　of　an　angle.
Parameters:
a　-　an　angle,　in　radians.
Returns:
the　cosine　of　the　argument

#p#副标题#e#

Cos函数返回三角的余弦函数，参数a是一个以double范例的弧度暗示的角值, 返回范例为double.

有人会问为什么不利用ScanndeRobot事件中的getRadarHeadingRadians()方 法直接获得弧度。哦，你来看看 Robocode中华同盟iiley的一段说明：

public　void　onScannedRobot(ScannedRobotEvent　event)　{
　 enemyX=Math.sin(Util.standardMathDirRadians (getRadarHeadingRadians()))*event.getDistance();
　 enemyY=Math.cos(Util.standardMathDirRadians (getRadarHeadingRadians()))*event.getDistance();
}

看起来仿佛正确的，可是你实践一下会发明他很禁绝确，为什么呢？原因在 于getRadarHeadingRadians()函数，当你挪用此函数的时候实际上雷达已经不在 方才扫描到仇人的谁人角度了，他已经转过了十几度甚至更多。雷达默认动弹速 度是45度/robocode单元时间，实际上一般来说你用getRadarHeadingRadians() 获得的值老是45度的整数倍。（一些环境除外，好比说你用了turnRadarLeft (11)雷同的语句今后）。

#p#分页标题#e#

Robocode 也遵循数学应用中的根基法例用两种要领来暗示偏向的角度：角度 制和弧度制，本文的代码及以前文章中的代码我们一直用的是角度制。别的一种 要领就是操作 ScannedRobotEvent.getBearingRadians() +robot.getHeadingRadians()获得仇人以弧度暗示的偏向，这个要领在本文章中 没有说明白，有乐趣的伴侣可以本身试试用Java.util 类库来实现. 也可参考文 档 "准确计较仇人的坐标"。各人也可较量两种要领各自特点，这将是个很有意 思的进程。

移动锁定

虽然，纵然是最简朴的呆板人也不会坐在那一动不动等着你来没落。它会躲 避你的打击以及扫描，当你向它本来坐标处开火，说不定它已经跑得老远了，当 然这一切都不是我们所但愿看到的。我们的目标是要没落它:不管他是移动或静 止的。下面我们就团结偏向系统与坐标系统，来锁定我们移动的方针。缔造一个 我们本身的高级扫描呆板人。发起你在此处下载源代码( resource)并看看演示 结果再回到我们的文章中来。显示如图5：

图5

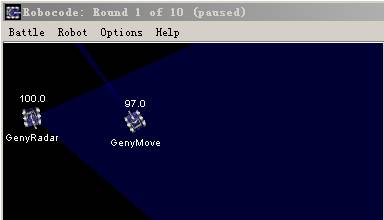
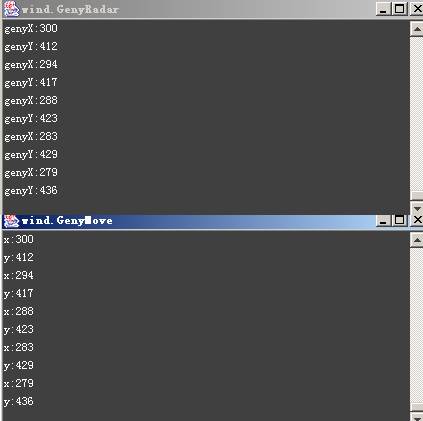
Robocode根本原理之坐标锁定

Robocode根本原理之坐标锁定

#p#副标题#e#

比拟一下上面的数据，不管方针GenyMove在哪GenyRadar都能获得它准确的坐 标。是不是有一种成绩感！是的，仇人已经完全在我们的把握之中。纵然它在移 动中也无法挣脱我们雷达的扫描节制。这里只是很简朴举了一些例子，GenyMove 在每一个时间周期（有关时间周期的说明见的 Rock ’em, sock ’em Robocode: Round2）移动本身的位置并打印出移动后的坐标，而GenyRadar扫描系统不断的 扫描方针，并一直追踪，同时打印出扫描到的GenyMove方位。要害部门在我们的 ScannedRobotEvent事件如列表3

列表3:

　public　void　onScannedRobot(　ScannedRobotEvent　 e　)
　　 {
　　　　 double　heading　=　e.getBearing()　+getHeading();
　　　　 double　distance　=　e.getDistance();　//求得间隔
　　　　 double　ager_bearing　=　Math.toRadians(heading　%　360);　 //角度转为弧度
　　　　 double　genyX　=　getX()　+　Math.sin(ager_bearing)　*　 distance;
　　　　 double　genyY　=　getY()　+　Math.cos(ager_bearing)　*　 distance;
　　　　 out.println("genyX:"+　Math.round(genyX));
　　　　 out.println("genyY:"+　Math.round(genyY));

　　　　 if(　heading　>=　360　)
　　　　　　 heading　=　heading　-　360;
　　　　 if(　heading　<　0　)
　　　　　　 heading　=　heading　+360;
　　　　 double　bearing　=　getRadarHeading()　-　heading;
　　　　 double　radar_degree;
　　　　 boolean　radar_direction;
　　　　 if(　0　<=　bearing　&&　bearing　<=　180　)
　　　　 {
　　　　　　 radar_direction　=　LEFT;
　　　　 }
　　　　 else　if(　bearing　<=　-180　)
　　　　 {
　　　　　　 radar_direction　=　LEFT;
　　　　　　 bearing　=　(　360　+　bearing　);
　　　　 }
　　　　 else　if(　bearing　<　0　)
　　　　 {
　　　　　　 radar_direction　=　RIGHT;
　　　　　　 bearing　=(　-bearing　);
　　　　 }
　　　　 else
　　　　 {
　　　　　　 radar_direction　=　RIGHT;
　　　　　　 bearing　=　(360　-　bearing);
　　　　 }
　　　　 radar_degree　=　bearing　*　1.3　;　//加大每一时间周期 (tick)的扫描范畴

　　　　 if(　radar_direction　==　RIGHT　)
　　　　 {
　　　　　　 setTurnRadarRight(　radar_degree　);
　　　　　　 execute();
　　　　 }
　　　　 else
　　　　 {
　　　　　　 setTurnRadarLeft(　radar_degree　);
　　　　　　 execute();
　　　　 }

我们在代码中首先求得GenyMove的绝对角度，然后用扫描时雷达的绝对角度 减去方针GenyMove的角度求得两者的角度差也即我们雷达要旋转的角度。最后利 用一个小能力radar_degree = bearing * 1.3 使雷达在方针的范畴阁下摆动以 扩大雷达扫描区域.这样不管方针往哪边移动都在本身的雷达扫描区内。

#p#分页标题#e#

在此没有举办很具体的讲授了，我想凭你学到的偏向及坐标常识很快能大白 其中道理并设计出本身的高级扫描呆板人来。智慧的你大概会兴奋的想，哈，我 的炮管用沟通的步伐锁定方针，这样仇人不就没步伐跑了，被我追着打。谜底是 错误的，雷达的扫描是条长线能直接定位到方针上，它到方针的时间差险些为零 ，而且雷达的扫描范畴比炮管大且准确。而炮管每时间周期只有20度，它定位目 标是依靠着子弹,只有子弹打中了方针，才气说炮管的计较坐标是准确的。可是 由于子弹达到方针位置时需要必然的时间差，子弹自己又有速度值（20-3*power ），所以要想炮管锁定方针并让子弹击中方针，我们还得颠末准确的计较,并要 预测方针大概的动作：是直线前进，照旧做圆周举动，照旧随机举动等等。这些 都是我们要充实思量的因素。是不是很有挑战性!这一切都在Robocode的世界中 期待着您的缔造！

#p#副标题#e#

三角函数基本

下面我们只是很简朴的先容了一下与Robocode相关的三角函数常识，要想了 解具体的，各人可从家中高中代数与几许书中获得这一切。

1．角的观念

在平面内，角可以看作一条射线绕着它的端点旋转而成的图形。如图，一条 射线由本来的位置OA，绕着它的端点O按逆时偏向旋转到另一位置OB，就形成角 a.旋转开始时的射线OA叫做角a的始边，旋转终止时的射线OB叫做角a的终边，射 线的端点O叫做角a的极点。习惯上，我们把按逆时针偏向旋转而成的角叫做正角 ；按顺时针偏向旋转而成的角叫做负角.所有与a终边沟通的角包罗a在内，可以 用式子暗示：a+K*360度,对应到Robocode的偏向系统中，只要我们以呆板人的 heading偏向做射线，耽误到与屏幕交点处的角度就是我们呆板人的heading角度 。

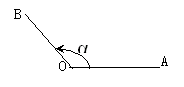
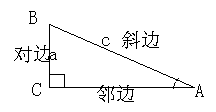
Robocode根本原理之坐标锁定

2.直角三角函数

在△ABC中，∠a为直角，我们把锐角A的对边与斜边的比叫做∠A的正弦，记 作sina；锐角a的邻边与斜边的比叫做∠a的余弦，记作cosa，即

sina=对边BC/斜边AB

cosa=邻边AC/斜边AB

Robocode根本原理之坐标锁定

3.单元圆和三角函数线

半径为1的圆叫做单元圆。设单元圆的圆心与坐标原点重合，则单元圆与x轴 的交点分为别为A（1,0）、A′(－1,0)，与y轴的交点别离为B(0,1)、 B′(0,－ 1)。设角a的极点在圆心O，始点与x轴的正半轴重合，终边与单元圆相交于点P， 过点P作PM垂直x轴于M，则由直角三角函数的界说可知:OM=cosa，MP=sina ，点P 的坐标为(cosa，sina)，即P(cosa，sina)。个中cosa＝OM*1，sina＝MP*1。 Robocode中所有有关的坐标都可用这种要领求得。

4．弧度制

费用做单元来怀抱角的制度叫做角度制。数学和其他科学研究中常用另一种 怀抱角的制度―弧度制。以角的极点为圆心，以任意长的半径作圆把这个角所对 的弧长与半径的比来权衡角的制度叫做弧度制.长度便是半径的弧长叫1弧度。这 段弧所对的圆心角的巨细也是1弧度。凡是单元“弧度”省略不写。例：弧长为 1.3325。单元就是弧度。由角度和弧度两种单元之间的干系获得:2π弧度=360度 ,2/3π弧度=270度,π弧度=180度,1/2π弧度=90 度,并可推出1弧度 = 360度/2 π = 57°即 1弧度=角度*180/Math.PI.

一般划定：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零 。这样角的荟萃与实数荟萃的元素就成立起了“一一对应”的干系。

哦，终于完了。到此为止，我们进修了Robocode根基道理中的偏向系统和坐 标系统，当你对这两个观念有必然的相识，你就可以建设本身的呆板人，在战争 的洗礼中不绝完善本身的呆板人，并适当的在你的呆板人插手一些经典的战斗策 略。它将越来越完美。不外不要忘了，必然要插手呆板人的智能进修本领,只有 具有超强进修本领的呆板人才气无敌于天下，在下一篇我们将会看到一个高智能 的呆板人。

    关键字：

在线提交作业