总结Trie树
今天本文的学习主要是讨论一棵简单的trie树,基于英文字母26个字母组成,讨论插入字符串、判断前缀是否存在、查找字符串等基本操作,有需要的朋友可以参考学习一下。
Trie树,又称字典树,单词查找树或者前缀树,是一种用于快速检索的多叉树结构,如英文字母的字典树是一个26叉树。Trie一词来自retrieve,发音为/tri:/ “tree”,也有人读为/tra?/ “try”。
Trie树可以利用字符串的公共前缀来节约存储空间。如下图所示,该trie树用10个节点保存了6个字符串tea,ten,to,in,inn,int:
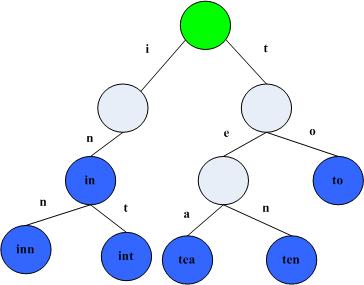
在该trie树中,字符串in,inn和int的公共前缀是“in”,因此可以只存储一份“in”以节省空间。当然,如果系统中存在大量字符串且这些字符串基本没有公共前缀,则相应的trie树将非常消耗内存,这也是trie树的一个缺点。
Trie树的基本性质可以归纳为:
1.根节点不包含字符,除根节点意外每个节点只包含一个字符。
2.从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
3.每个节点的所有子节点包含的字符串不相同。
如图所示,该trie树存有abc、d、da、dda四个字符串,如果是字符串会在节点的尾部进行标记。没有后续字符的branch分支指向NULL。
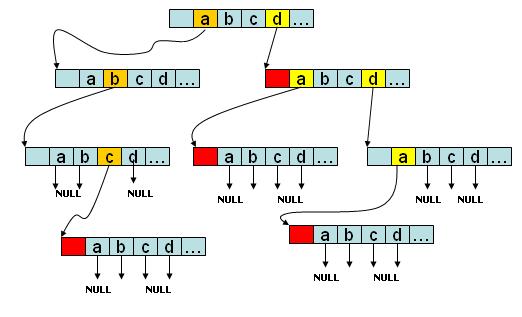
Trie的优点举例
已知n个由小写字母构成的平均长度为10的单词,判断其中是否存在某个串为另一个串的前缀子串。下面对比3种方法:
1. 最容易想到的:即从字符串集中从头往后搜,看每个字符串是否为字符串集中某个字符串的前缀,复杂度为O(n^2)。
2. 使用hash:我们用hash存下所有字符串的所有的前缀子串。建立存有子串hash的复杂度为O(n*len)。查询的复杂度为O(n)* O(1)= O(n)。
3. 使用trie:因为当查询如字符串abc是否为某个字符串的前缀时,显然以b,c,d….等不是以a开头的字符串就不用查找了。所以建立trie的复杂度为O(n*len),而建立+查询在trie中是可以同时执行的,建立的过程也就可以成为查询的过程,hash就不能实现这个功能。所以总的复杂度为O(n*len),实际查询的复杂度只是O(len)。
解释一下hash为什么不能将建立与查询同时执行,例如有串:911,911456输入,如果要同时执行建立与查询,过程就是查询911,没有,然后存入9、91、911,查询911456,没有然后存入9114、91145、911456,而程序没有记忆功能,并不知道911在输入数据中出现过。所以用hash必须先存入所有子串,然后for循环查询。
而trie树便可以,存入911后,已经记录911为出现的字符串,在存入911456的过程中就能发现而输出答案;倒过来亦可以,先存入911456,在存入911时,当指针指向最后一个1时,程序会发现这个1已经存在,说明911必定是某个字符串的前缀。
Trie树的操作
在Trie树中主要有3个操作,插入、查找和删除。一般情况下Trie树中很少存在删除单独某个结点的情况,因此只考虑删除整棵树。
1.插入
假设存在字符串str,Trie树的根结点为root。i=0,p=root。
1)取str[i],判断p->next[str[i]-97]是否为空,若为空,则建立结点temp,并将p->next[str[i]-97]指向temp,然后p指向temp;
若不为空,则p=p->next[str[i]-97];
2)i++,继续取str[i],循环1)中的操作,直到遇到结束符'\\0',此时将当前结点p中的isStr置为true。
2.查找
假设要查找的字符串为str,Trie树的根结点为root,i=0,p=root
1)取str[i],判断判断p->next[str[i]-97]是否为空,若为空,则返回false;若不为空,则p=p->next[str[i]-97],继续取字符。
2)重复1)中的操作直到遇到结束符'\\0',若当前结点p不为空并且isStr为true,则返回true,否则返回false。
3.删除
删除可以以递归的形式进行删除。
Trie的简单实现(插入、查询)。
1
2#include <iostream>
3using namespace std;
4
5const int branchNum = 26; //声明常量
6int i;
7
8struct Trie_node
9{
10 bool isStr; //记录此处是否构成一个串。
11 Trie_node *next[branchNum];//指向各个子树的指针,下标0-25代表26字符
12 Trie_node():isStr(false)
13 {
14 memset(next,NULL,sizeof(next));
15 }
16};
17
18class Trie
19{
20public:
21 Trie();
22 void insert(const char* word);
23 bool search(char* word);
24 void deleteTrie(Trie_node *root);
25private:
26 Trie_node* root;
27};
28
29Trie::Trie()
30{
31 root = new Trie_node();
32}
33
34void Trie::insert(const char* word)
35{
36 Trie_node *location = root;
37 while(*word)
38 {
39 if(location->next[*word-'a'] == NULL)//不存在则建立
40 {
41 Trie_node *tmp = new Trie_node();
42 location->next[*word-'a'] = tmp;
43 }
44 location = location->next[*word-'a']; //每插入一步,相当于有一个新串经过,指针要向下移动
45 word++;
46 }
47 location->isStr = true; //到达尾部,标记一个串
48}
49
50bool Trie::search(char *word)
51{
52 Trie_node *location = root;
53 while(*word && location)
54 {
55 location = location->next[*word-'a'];
56 word++;
57 }
58 return(location!=NULL && location->isStr);
59}
60
61void Trie::deleteTrie(Trie_node *root)
62{
63 for(i = 0; i < branchNum; i++)
64 {
65 if(root->next[i] != NULL)
66 {
67 deleteTrie(root->next[i]);
68 }
69 }
70 delete root;
71}
72
73void main() //简单测试
74{
75 Trie t;
76 t.insert(“a”);
77 t.insert(“abandon”);
78 char * c = “abandoned”;
79 t.insert(c);
80 t.insert(“abashed”);
81 if(t.search(“abashed”))
82 printf(“true\\n”);
83}
Trie树是一种非常重要的数据结构,它在信息检索,字符串匹配等领域有广泛的应用,同时,它也是很多算法和复杂数据结构的基础,如后缀树,AC自动机等,因此,掌握Trie树这种数据结构,对于一名IT人员,显得非常基础且必要!如果您喜欢我们的分享,那就关注课课家吧!
