全面教你用Spark学习矩阵分解推荐算法

     今天，课课家来一起和大家讨论“用Spark学习矩阵分解推荐算法”，有需要的小伙伴，可以参考一下，如果有更高的见解，也可以交流一下。一定要认真的阅读课文哦！

在矩阵分解在协同过滤推荐算法中的应用中，我们对矩阵分解在推荐算法中的应用原理做了总结，这里我们就从实践的角度来用Spark学习矩阵分解推荐算法。

　　1. Spark推荐算法概述

　　在Spark MLlib中，推荐算法这块只实现了基于矩阵分解的协同过滤推荐算法。而基于的算法是FunkSVD算法，即将m个用户和n个物品对应的评分矩阵M分解为两个低维的矩阵：

　　

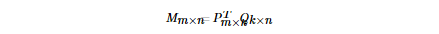
　　其中k为分解成低维的维数，一般远比m和n小。如果大家对FunkSVD算法不熟悉，可以复习对应的原理篇。

　　2. Spark推荐算法类库介绍

　　在Spark MLlib中，实现的FunkSVD算法支持Python,java,Scala和R的接口。由于前面的实践篇我们都是基于Python，本文的后面的介绍和使用也会使用MLlib的Python接口。

　　Spark MLlib推荐算法python对应的接口都在pyspark.mllib.recommendation包中，这个包有三个类，Rating, MatrixFactorizationModel和ALS。虽然里面有三个类，但是算法只是FunkSVD算法。下面介绍这三个类的用途。

　　Rating类比较简单，仅仅只是为了封装用户，物品与评分这3个值。也就是说，Rating类里面只有用户，物品与评分三元组， 并没有什么函数接口。

　　ALS负责训练我们的FunkSVD模型。之所以这儿用交替最小二乘法ALS表示，是因为Spark在FunkSVD的矩阵分解的目标函数优化时，使用的是ALS。ALS函数有两个函数，一个是train,这个函数直接使用我们的评分矩阵来训练数据，而另一个函数trainImplicit则稍微复杂一点，它使用隐式反馈数据来训练模型，和train函数相比，它多了一个指定隐式反馈信心阈值的参数，比如我们可以将评分矩阵转化为反馈数据矩阵，将对应的评分值根据一定的反馈原则转化为信心权重值。由于隐式反馈原则一般要根据具体的问题和数据来定，本文后面只讨论普通的评分矩阵分解。

　　MatrixFactorizationModel类是我们用ALS类训练出来的模型，这个模型可以帮助我们做预测。常用的预测有某一用户和某一物品对应的评分，某用户最喜欢的N个物品，某物品可能会被最喜欢的N个用户，所有用户各自最喜欢的N物品，以及所有物品被最喜欢的N个用户。

　　对于这些类的用法我们再后面会有例子讲解。

　　3. Spark推荐算法重要类参数

　　这里我们再对ALS训练模型时的重要参数做一个总结。

　　1) ratings : 评分矩阵对应的RDD。需要我们输入。如果是隐式反馈，则是评分矩阵对应的隐式反馈矩阵。

　　2) rank : 矩阵分解时对应的低维的维数。即PTm×kQk×nPm×kTQk×n中的维度k。这个值会影响矩阵分解的性能，越大则算法运行的时间和占用的内存可能会越多。通常需要进行调参，一般可以取10-200之间的数。

　　3) iterations :在矩阵分解用交替最小二乘法求解时，进行迭代的最大次数。这个值取决于评分矩阵的维度，以及评分矩阵的系数程度。一般来说，不需要太大，比如5-20次即可。默认值是5。

　　4) lambda: 在 python接口中使用的是lambda_,原因是lambda是Python的保留字。这个值即为FunkSVD分解时对应的正则化系数。主要用于控制模型的拟合程度，增强模型泛化能力。取值越大，则正则化惩罚越强。大型推荐系统一般需要调参得到合适的值。

　　5) Alpha : 这个参数仅仅在使用隐式反馈trainImplicit时有用。指定了隐式反馈信心阈值，这个值越大则越认为用户和他没有评分的物品之间没有关联。一般需要调参得到合适值。

　　从上面的描述可以看出，使用ALS算法还是蛮简单的，需要注意调参的参数主要的是矩阵分解的维数rank, 正则化超参数lambda。如果是隐式反馈，还需要调参隐式反馈信心阈值alpha 。

　　4. Spark推荐算法实例

　　下面我们用一个具体的例子来讲述Spark矩阵分解推荐算法的使用。

　　这里我们使用MovieLens 100K的数据。

　　将数据解压后，我们只使用其中的u.data文件中的评分数据。这个数据集每行有4列，分别对应用户ID，物品ID，评分和时间戳。由于我的机器比较破，在下面的例子中，我只使用了前100条数据。因此如果你使用了所有的数据，后面的预测结果会与我的不同。

　　协同过滤

#p#分页标题#e#

　　协同过滤（CollaborativeFiltering，简称CF，WIKI上的定义是：简单来说是利用某个兴趣相投、拥有共同经验之群体的喜好来推荐感兴趣的资讯给使用者，个人透过合作的机制给予资讯相当程度的回应（如评分）并记录下来以达到过滤的目的，进而帮助别人筛选资讯，回应不一定局限于特别感兴趣的，特别不感兴趣资讯的纪录也相当重要。

　　协同过滤常被应用于推荐系统。这些技术旨在补充用户—商品关联矩阵中所缺失的部分。

　　MLlib当前支持基于模型的协同过滤，其中用户和商品通过一小组隐性因子进行表达，并且这些因子也用于预测缺失的元素。MLLib使用交替最小二乘法（ALS）来学习这些隐性因子。

　　用户对物品或者信息的偏好，根据应用本身的不同，可能包括用户对物品的评分、用户查看物品的记录、用户的购买记录等。其实这些用户的偏好信息可以分为两类：

　　l显式的用户反馈：这类是用户在网站上自然浏览或者使用网站以外，显式地提供反馈信息，例如用户对物品的评分或者对物品的评论。

　　l隐式的用户反馈：这类是用户在使用网站是产生的数据，隐式地反映了用户对物品的喜好，例如用户购买了某物品，用户查看了某物品的信息，等等。

　　（1）显式的用户反馈能准确地反映用户对物品的真实喜好，但需要用户付出额外的代价；而隐式的用户行为，通过一些分析和处理，也能反映用户的喜好，只是数据不是很精确，有些行为的分析存在较大的噪音。但只要选择正确的行为特征，隐式的用户反馈也能得到很好的效果，只是行为特征的选择可能在不同的应用中有很大的不同，例如在电子商务的网站上，购买行为其实就是一个能很好表现用户喜好的隐式反馈。

　　（2）推荐引擎根据不同的推荐机制可能用到数据源中的一部分，然后根据这些数据，分析出一定的规则或者直接对用户对其他物品的喜好进行预测计算。这样推荐引擎可以在用户进入时给他推荐他可能感兴趣的物品。

　　（3）MLlib目前支持基于协同过滤的模型，在这个模型里，用户和产品被一组可以用来预测缺失项目的潜在因子来描述。特别是我们实现交替最小二乘（ALS）算法来学习这些潜在的因子，在MLlib中的实现有如下参数：

　　lnumBlocks是用于并行化计算的分块个数（设置为-1时为自动配置）；

　　lrank是模型中隐性因子的个数；

　　literations是迭代的次数；

　　llambda是ALS的正则化参数；

　　limplicitPrefs决定了是用显性反馈ALS的版本还是用隐性反馈数据集的版本；

　　lalpha是一个针对于隐性反馈ALS版本的参数，这个参数决定了偏好行为强度的基准。

　　首先需要要确保你安装好了Hadoop和Spark(版本不小于1.6)，并设置好了环境变量。一般我们都是在ipython notebook(jupyter notebook)中学习，所以最好把基于notebook的Spark环境搭好。当然不搭notebook的Spark环境也没有关系，只是每次需要在运行前设置环境变量。

　　如果你没有搭notebook的Spark环境，则需要先跑下面这段代码。当然，如果你已经搭好了，则下面这段代码不用跑了。

　　在跑算法之前，建议输出Spark Context如下，如果可以正常打印内存地址，则说明Spark的运行环境搞定了。

　　print sc

　　比如我的输出是：

　　首先我们将u.data文件读入内存，并尝试输出第一行的数据来检验是否成功读入，注意复制代码的时候，数据的目录要用你自己的u.data的目录。代码如下：

　　输出如下：

　　u’196\\t242\\t3\\t881250949′

　　可以看到数据是用\\t分开的，我们需要将每行的字符串划开，成为数组，并只取前三列，不要时间戳那一列。代码如下：

　　输出如下：

　　[u’196′, u’242′, u’3′]

#p#分页标题#e#

　　此时虽然我们已经得到了评分矩阵数组对应的RDD，但是这些数据都还是字符串，Spark需要的是若干Rating类对应的数组。因此我们现在将RDD的数据类型做转化，代码如下：

　　输出如下：

　　Rating(user=196, product=242, rating=3.0)

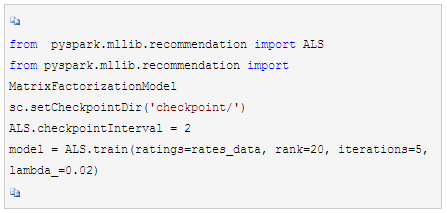
　　可见我们的数据已经是基于Rating类的RDD了，现在我们终于可以把整理好的数据拿来训练了，代码如下, 我们将矩阵分解的维度设置为20，最大迭代次数设置为5，而正则化系数设置为0.02。在实际应用中，我们需要通过交叉验证来选择合适的矩阵分解维度与正则化系数。这里我们由于是实例，就简化了。

　　将模型训练完毕后，我们终于可以来做推荐系统的预测了。

　　首先做一个最简单的预测，比如预测用户38对物品20的评分。代码如下：

　　print model.predict(38,20)

　　输出如下：

　　0.311633491603

　　可见评分并不高。

　　现在我们来预测了用户38最喜欢的10个物品，代码如下：

　　print model.recommendProducts(38,10)

　　输出如下：

　　[ Rating(user=38, product=95, rating=4.995227969811873),

　　Rating(user=38, product=304, rating=2.5159673379104484),

　　Rating(user=38, product=1014, rating=2.165428673820349),

　　Rating(user=38, product=322, rating=1.7002266119079879),

　　Rating(user=38, product=111, rating=1.2057528774266673),

　　Rating(user=38, product=196, rating=1.0612630766055788),

　　Rating(user=38, product=23, rating=1.0590775012913558),

　　Rating(user=38, product=327, rating=1.0335651317559753),

　　Rating(user=38, product=98, rating=0.9677333686628911),

　　Rating(user=38, product=181, rating=0.8536682271006641)]

　　可以看出用户38可能喜欢的对应评分从高到低的10个物品。

　　接着我们来预测下物品20可能最值得推荐的10个用户，代码如下：

　　print model.recommendUsers(20,10)

　　输出如下：

　　[ Rating(user=115, product=20, rating=2.9892138653406635),

　　Rating(user=25, product=20, rating=1.7558472892444517),

　　Rating(user=7, product=20, rating=1.523935609195585),

　　Rating(user=286, product=20, rating=1.3746309116764184),

　　Rating(user=222, product=20, rating=1.313891405211581),

　　Rating(user=135, product=20, rating=1.254412853860262),

　　Rating(user=186, product=20, rating=1.2194811581542384),

　　Rating(user=72, product=20, rating=1.1651855319930426),

　　Rating(user=241, product=20, rating=1.0863391992741023),

　　Rating(user=160, product=20, rating=1.072353288848142)]

　　现在我们来看看每个用户最值得推荐的三个物品，代码如下:

　　print model.recommendProductsForUsers(3).collect()

　　由于输出非常长，这里就不将输出copy过来了。

　　而每个物品最值得被推荐的三个用户，代码如下：

　　print model.recommendUsersForProducts(3).collect()

　　同样由于输出非常长，这里就不将输出copy过来了。

     结束语：看文章的小伙伴，觉得还清楚吧！上面举得例子，小伙伴们了解么？如果还想了解更多关于这方面的知识，随时可以登陆课课家，这里面有全面的知识内容还有视频教学，随时欢迎你的到来。